Page 12 - DCAP407_DATA_STRUCTURE

Unit 1: Introduction to Data Structures

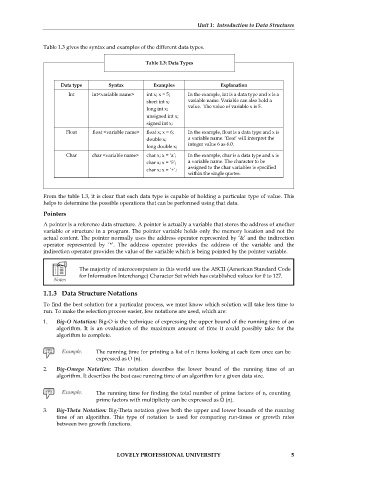
Table 1.3 gives the syntax and examples of the different data types.

Table 1.3: Data Types

Data type Syntax Examples Explanation
Int int<variable name> int x; x = 5; In the example, int is a data type and x is a
short int x; variable name. Variable can also hold a
long int x; value. The value of variable x is 5.
unsigned int x;
signed int x;
Float float <variable name> float x; x = 6; In the example, float is a data type and x is
double x; a variable name. ‘float’ will interpret the
long double x; integer value 6 as 6.0.
Char char <variable name> char x; x = ‘a’; In the example, char is a data type and x is
char x; x = ‘5’; a variable name. The character to be
char x; x = ‘+’; assigned to the char variables is specified
within the single quotes.

From the table 1.3, it is clear that each data type is capable of holding a particular type of value. This
helps to determine the possible operations that can be performed using that data.
Pointers

A pointer is a reference data structure. A pointer is actually a variable that stores the address of another
variable or structure in a program. The pointer variable holds only the memory location and not the
actual content. The pointer normally uses the address operator represented by ‘&’ and the indirection
operator represented by ‘*’. The address operator provides the address of the variable and the
indirection operator provides the value of the variable which is being pointed by the pointer variable.

The majority of microcomputers in this world use the ASCII (American Standard Code
for Information Interchange) Character Set which has established values for 0 to 127.

1.1.3 Data Structure Notations
To find the best solution for a particular process, we must know which solution will take less time to
run. To make the selection process easier, few notations are used, which are:

1. Big-O Notation: Big-O is the technique of expressing the upper bound of the running time of an
algorithm. It is an evaluation of the maximum amount of time it could possibly take for the
algorithm to complete.

The running time for printing a list of n items looking at each item once can be
expressed as O (n).
2. Big-Omega Notation: This notation describes the lower bound of the running time of an
algorithm. It describes the best case running time of an algorithm for a given data size.

The running time for finding the total number of prime factors of n, counting
prime factors with multiplicity can be expressed as Ω (n).
3. Big-Theta Notation: Big-Theta notation gives both the upper and lower bounds of the running
time of an algorithm. This type of notation is used for comparing run-times or growth rates
between two growth functions.

LOVELY PROFESSIONAL UNIVERSITY 5