Page 14 - DMTH201_Basic Mathematics-1

Unit 1: Trigonometric Functions-I

We’re now ready to look at sine and cosine as functions. Notes
Sine is an odd function, and cosine is an even function. You may not have come across these
adjectives “odd” and “even” when applied to functions, but it’s important to know them. A function
f is said to be an odd function if for any number x, f(–x) = –f(x). A function f is said to be an even
function if for any number x, f(–x) = f(x). Most functions are neither odd nor even functions, but it’s
important to notice when a function is odd or even. Any polynomial with only odd degree terms is
3
5
an odd function, for example, f(x) = x + 8x – 2x. (Note that all the powers of are odd numbers.)
Similarly, any polynomial with only even degree terms is an even function. For example, f(x) =
0
2
x – 3x – 5. (The constant 5 is 5x , and 0 is an even number.)
4
Sine is an odd function, and cosine is even
sin –t = –sin t,
and cos –t = cos t.
These facts follow from the symmetry of the unit circle across the -axis. The angle – is the same
angle as except it’s on the other side of the -axis. Flipping a point ( , ) to the other side of
the -axis makes it into ( ,– ), so the -coordinate is negated, that is, the sine is negated, but the
x-coordinate remains the same, that is, the cosine is unchanged.

An obvious property of sines and cosines is that their values lie between –1 and 1. Every point on
the unit circle is 1 unit from the origin, so the coordinates of any point are within 1 of 0 as well.

1.3.1 The Graphs of the Sine and Cosine Functions

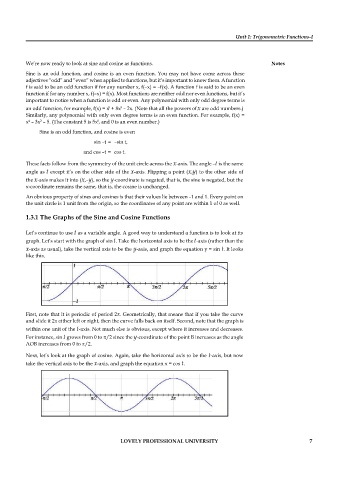
Let’s continue to use as a variable angle. A good way to understand a function is to look at its
graph. Let’s start with the graph of sin . Take the horizontal axis to be the -axis (rather than the
-axis as usual), take the vertical axis to be the -axis, and graph the equation y = sin . It looks
like this.

First, note that it is periodic of period 2 . Geometrically, that means that if you take the curve
and slide it 2 either left or right, then the curve falls back on itself. Second, note that the graph is
within one unit of the -axis. Not much else is obvious, except where it increases and decreases.
For instance, sin grows from 0 to /2 since the -coordinate of the point B increases as the angle
AOB increases from 0 to /2.

Next, let’s look at the graph of cosine. Again, take the horizontal axis to be the -axis, but now
take the vertical axis to be the -axis, and graph the equation x = cos .

LOVELY PROFESSIONAL UNIVERSITY 7