Page 78 - DMGT207_MANAGEMENT_OF_FINANCES

Unit 4: Risk and Return Analysis

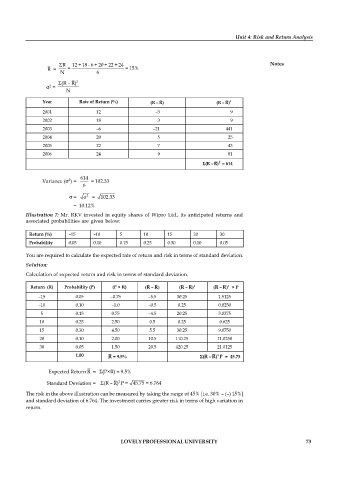
ΣR 12 + 18 - 6 + 20 + 22 + 24 Notes
R = = = 15%
N 6
Σ(R – R) 2
2
 =
N
Year Rate of Return (%) (R – R) (R – R)
2
2001 12 –3 9
2002 18 3 9
2003 –6 –21 441
2004 20 5 25
2005 22 7 43
2006 24 9 81
Σ(R – R) = 614
2

614
2
Variance ( ) = = 102.33
6
2
 = σ = 102.33
= 10.12%
Illustration 7: Mr. RKV invested in equity shares of Wipro Ltd., its anticipated returns and
associated probabilities are given below:

Return (%) –15 –10 5 10 15 20 30
Probability 0.05 0.10 0.15 0.25 0.30 0.10 0.05

You are required to calculate the expected rate of return and risk in terms of standard deviation.
Solution:
Calculation of expected return and risk in terms of standard deviation.
2
Return (R) Probability (P) (P × R) (R –R (R –R (R –R × P
2
)
)
)
–15 0.05 –0.75 –5.5 30.25 1.5125
–10 0.10 –1.0 –0.5 0.25 0.0250
5 0.15 0.75 –4.5 20.25 3.0375
10 0.25 2.50 0.5 0.25 0.625
15 0.30 4.50 5.5 30.25 9.0750
20 0.10 2.00 10.5 110.25 11.0250
30 0.05 1.50 20.5 420.25 21.0125
1.00 R = 9.5% Σ(R –R P = 45.75
2
)

Expected Return R = (P×R) = 9.5%
2
Standard Deviation = Σ(R – R) P = 45.75 = 6.764
The risk in the above illustration can be measured by taking the range of 45% [i.e. 30% – (–) 15%]
and standard deviation of 6.764. The investment carries greater risk in terms of high variation in
return.

LOVELY PROFESSIONAL UNIVERSITY 73