Page 200 - DMGT404 RESEARCH_METHODOLOGY

Research Methodology

Notes Kernel Estimation

The kernel regression is a non-parametric technique in statistics to estimate the conditional
expectation of a random variable. The objective is to find a non-linear relation between a pair of
random variables X and Y.
In any non-parametric regression, the conditional expectation of a variable Y relative to a
variable X may be written:
E(Y|X) = m(X)
where m is an unknown function.

Local Polynomial Regression

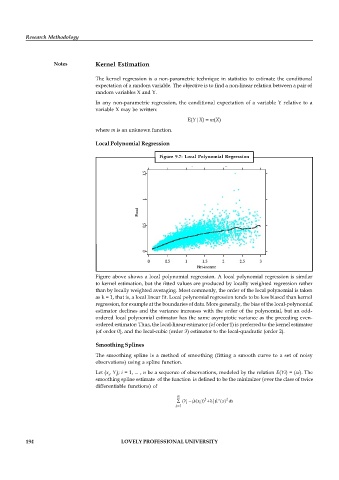
Figure 9.7: Local Polynomial Regression

Figure above shows a local polynomial regression. A local polynomial regression is similar
to kernel estimation, but the fitted values are produced by locally weighted regression rather
than by locally weighted averaging. Most commonly, the order of the local polynomial is taken
as k = 1, that is, a local linear fit. Local polynomial regression tends to be less biased than kernel
regression, for example at the boundaries of data. More generally, the bias of the local-polynomial
estimator declines and the variance increases with the order of the polynomial, but an odd-
ordered local polynomial estimator has the same asymptotic variance as the preceding even-
ordered estimator: Thus, the local-linear estimator (of order 1) is preferred to the kernel estimator
(of order 0), and the local-cubic (order 3) estimator to the local-quadratic (order 2).

Smoothing Splines
The smoothing spline is a method of smoothing (fitting a smooth curve to a set of noisy
observations) using a spline function.
Let (x , Y ); i = 1, ... , n be a sequence of observations, modeled by the relation E(Yi) = (xi). The
i i
smoothing spline estimate of the function is defined to be the minimizer (over the class of twice
differentiable functions) of
n
å (Y i - m x i 2 ˆ "( )x dx
2
ˆ ( )) +l m ò
 i 1

194 LOVELY PROFESSIONAL UNIVERSITY