Page 197 - DMGT404 RESEARCH_METHODOLOGY
P. 197
Unit 9: Correlation and Regression
Notes
) .
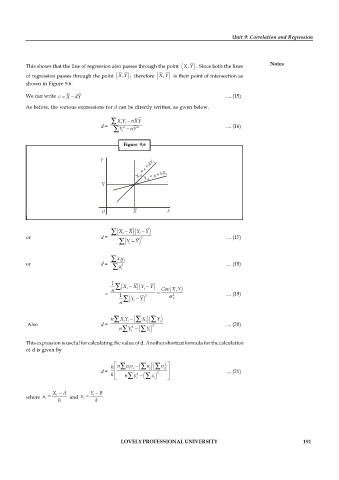
This shows that the line of regression also passes through the point ( ,X Y Since both the lines
)
of regression passes through the point ( ,X Y ) , therefore ( ,X Y is their point of intersection as
shown in Figure 9.6.
We can write c X - dY .... (15)
As before, the various expressions for d can be directly written, as given below.
å X Y - nXY
i
i
d = å Y - nY 2 .... (16)
2
i
Figure 9.6
Y dY i
c +
=
= +
X ci Y a bX i
ci
Y
O X X
å (X - X Y - Y )
)( i
i
or d = 2 .... (17)
å ( i Y )
Y -
å x y
or d = å y i i 2 i .... (18)
1 å (X - X Y - Y )
n i )( i Cov ( ,X Y )
= 1 å Y - ) 2 s 2 .... (19)
n ( i Y Y
nå X Y - (å X )(å Y )
i i i i
Also d = 2 .... (20)
nå Y - (å Y )
2
i i
This expression is useful for calculating the value of d. Another shortcut formula for the calculation
of d is given by
é nå (å )(å ) ù
h ê u v - u i v i ú
i i
d = .... (21)
k ê nå v - (å ) 2 ú
2
ë i v i û
X - A Y - B
where u i and v i
i
i
h k
LOVELY PROFESSIONAL UNIVERSITY 191