Page 116 - DCOM203_DMGT204_QUANTITATIVE_TECHNIQUES_I
P. 116
Unit 6: Measures of Central Tendency
Remarks: If the most repeated values, in the above analysis table, were not adjacent, the Notes
distribution would have been bi-modal, i.e., having two modes.
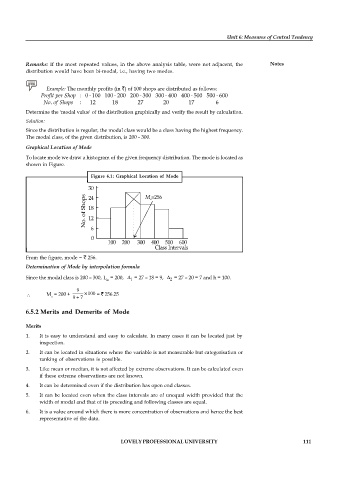
Example: The monthly profits (in ) of 100 shops are distributed as follows:
Profit per Shop : 0 -100 100 - 200 200 - 300 300 - 400 400 - 500 500 - 600
No. of Shops : 12 18 27 20 17 6
Determine the 'modal value' of the distribution graphically and verify the result by calculation.
Solution:
Since the distribution is regular, the modal class would be a class having the highest frequency.
The modal class, of the given distribution, is 200 - 300.
Graphical Location of Mode
To locate mode we draw a histogram of the given frequency distribution. The mode is located as
shown in Figure.
Figure 6.1: Graphical Location of Mode
From the figure, mode = 256.
Determination of Mode by interpolation formula
Since the modal class is 200 – 300, L = 200, 1 = 27 – 18 = 9, 2 = 27 – 20 = 7 and h = 100.
m
9
M = 200 + 100 = 256.25
o 9 7
6.5.2 Merits and Demerits of Mode
Merits
1. It is easy to understand and easy to calculate. In many cases it can be located just by
inspection.
2. It can be located in situations where the variable is not measurable but categorisation or
ranking of observations is possible.
3. Like mean or median, it is not affected by extreme observations. It can be calculated even
if these extreme observations are not known.
4. It can be determined even if the distribution has open end classes.
5. It can be located even when the class intervals are of unequal width provided that the
width of modal and that of its preceding and following classes are equal.
6. It is a value around which there is more concentration of observations and hence the best
representative of the data.
LOVELY PROFESSIONAL UNIVERSITY 111