Page 145 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 9: Correlation: Definition, Types and its Application for Economists

Notes
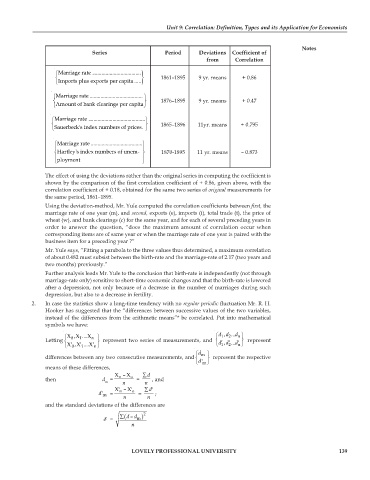
Series Period Deviations Coefficient of
from Correlation
⎧ ⎫Marriage rate ....................................
⎨ ⎬ 1861–1895 9 yr. means + 0.86
⎩ Imports plus exports per capita ..... ⎭

⎧ ⎫Marriage rate .......................................
⎨ ⎬ 1876–1895 9 yr. means + 0.47
⎩ Amount of bank clearings per capita ⎭

⎧ Marriage rate ..........................................⎫
⎨ ⎬ 1865–1896 11yr. means + 0.795
⎩ Sauerbeck's index numbers of prices. ⎭

⎧ ⎫Marriage rate ......................................
⎪ ⎪
⎨ ⎬ Hartley's index numbers of unem- 1870-1895 11 yr. means – 0.873
⎪ ⎪
⎩ ployment ⎭

The effect of using the deviations rather than the original series in computing the coefficient is
shown by the comparison of the first correlation coefficient of + 0.86, given above, with the
correlation coefficient of + 0.18, obtained for the same two series of original measurements for
the same period, 1861–1895.
Using the deviation-method, Mr. Yule computed the correlation coefficients between first, the
marriage rate of one year (m), and second, exports (e), imports (i), total trade (t), the price of
wheat (w), and bank clearings (c) for the same year, and for each of several preceding years in
order to answer the question, “does the maximum amount of correlation occur when
corresponding items are of same year or when the marriage rate of one year is paired with the
business item for a preceding year ?”
Mr. Yule says, “Fitting a parabola to the three values thus determined, a maximum correlation
of about 0.482 must subsist between the birth-rate and the marriage-rate of 2.17 (two years and
two months) previously.”
Further analysis leads Mr. Yule to the conclusion that birth-rate is independently (not through
marriage-rate only) sensitive to short-time economic changes and that the birth-rate is lowered
after a depression, not only because of a decrease in the number of marriages during such
depression, but also to a decrease in fertility.
2. In case the statistics show a long-time tendency with no regular periodic fluctuation Mr. R. H.
Hooker has suggested that the “differences between successive values of the two variables,
instead of the differences from the arithmetic means”* be correlated. Put into mathematical
symbols we have:
,
⎧ X ,X ....X n ⎫ ⎧ dd 2 ...d n ⎫
1
Letting ⎨ 0 1 ⎬ represent two series of measurements, and ⎨ dd′ , ′ ...d′ ⎬ represent
⎩ X' ,X' ....X' n ⎭ ⎩ 1 2 n ⎭
0
1
⎧ d ⎫ m
differences between any two consecutive measurements, and ⎨ ⎬ represent the respective
⎩ ' d ⎭ m
means of these differences,
X– X ∑d
then d = n o = , and
m n n
d
X' – X' ∑ '
' d m = n n o = n ;
and the standard deviations of the differences are
(
δ = ∑ dd m ) – 2
n

LOVELY PROFESSIONAL UNIVERSITY 139