Page 66 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Statistical Methods in Economics

Notes Calculation of Median in Discrete Series

Example 8: Find out the value of median from the following data:
Weekly Wages (Rs.) 100 50 70 110 80

Number of Workers 15 20 15 18 12

Solution: The data is first rearranged in ascending order (with respect to X).
X (ascending order) f Cumulative frequency c.f.

50 20 20
70 15 20 + 15 = 35
80 12 35 + 12 = 47
100 15 47 + 15 = 62
110 18 62 + 18 = 80

∑ f = 80

⎛ + ⎞ N1 th
M= ⎜ ⎟ item. Here N = ∑ f = 80.
⎝ 2 ⎠

⎛ + 1 81 ⎞ 80
∴ M= ⎜ ⎝ 2 = 2 ⎟ ⎠ = 40.5 item.
th
40.5th item would lie in the cumulative frequency (c.f.) 47. Therefore the Median = 80.
Answer: The median weekly wages = Rs. 80.
5.3 Application of Mode

A third type of “Central value” or “Centre” of the distribution is the value of greatest frequency or,
more precisely, of greatest frequency density. Graphically, it is the value on the X-axis below the
peak, or highest point of the frequency curve. This average is called the mode.
The mode is often said to be the value which occurs most frequently. While this statement is quite
helpful in interpreting the mode, it cannot safely be applied to any distribution, because of the vagaries
of sampling. Even fairly large samples drawn from a statistical population with a single well-defined
mode may exhibit very erratic fluctuations. Hence, mode should be thought as the value which has
the greatest density in its immediate neighbourhood. For this reason mode is also called the most typical
or fashionable value of a distribution.
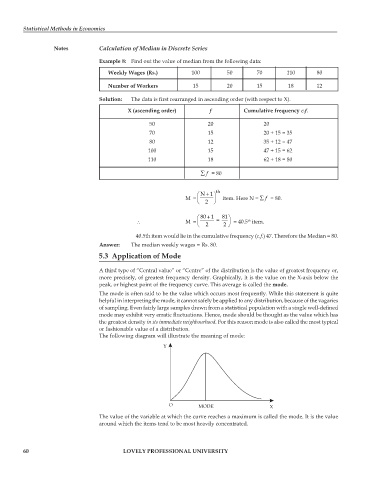
The following diagram will illustrate the meaning of mode:

Y

O MODE X
The value of the variable at which the curve reaches a maximum is called the mode. It is the value
around which the items tend to be most heavily concentrated.

60 LOVELY PROFESSIONAL UNIVERSITY