Page 67 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 5: Application of Mean, Median and Mode

Although mode is that value which occurs most frequently it does not follow that its frequency Notes
represents a majority out of all the total number of frequencies. For example, in the election of college
union president the votes obtained by three candidates contesting for presidentship out of a total of
816 votes polled are as follows:
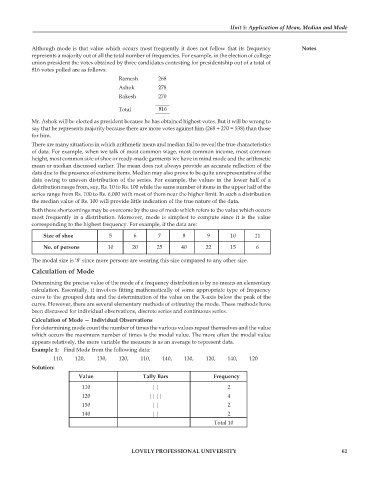
Ramesh 268
Ashok 278
Rakesh 270

Total 816
Mr. Ashok will be elected as president because he has obtained highest votes. But it will be wrong to
say that he represents majority because there are more votes against him (268 + 270 = 538) than those
for him.
There are many situations in which arithmetic mean and median fail to reveal the true characteristics
of data. For example, when we talk of most common wage, most common income, most common
height, most common size of shoe or ready-made garments we have in mind mode and the arithmetic
mean or median discussed earlier. The mean does not always provide an accurate reflection of the
data due to the presence of extreme items. Median may also prove to be quite unrepresentative of the
data owing to uneven distribution of the series. For example, the values in the lower half of a
distribution range from, say, Rs. 10 to Rs. 100 while the same number of items in the upper half of the
series range from Rs. 100 to Rs. 6,000 with most of them near the higher limit. In such a distribution
the median value of Rs. 100 will provide little indication of the true nature of the data.
Both these shortcomings may be overcome by the use of mode which refers to the value which occurs
most frequently in a distribution. Moreover, mode is simplest to compute since it is the value
corresponding to the highest frequency. For example, if the data are:
Size of shoe 5 6 7 8 9 10 11
No. of persons 10 20 25 40 22 15 6

The modal size is ‘8’ since more persons are wearing this size compared to any other size.
Calculation of Mode

Determining the precise value of the mode of a frequency distribution is by no means an elementary
calculation. Essentially, it involves fitting mathematically of some appropriate type of frequency
curve to the grouped data and the determination of the value on the X-axis below the peak of the
curve. However, there are several elementary methods of estimating the mode. These methods have
been discussed for individual observations, discrete series and continuous series.
Calculation of Mode — Individual Observations
For determining mode count the number of times the various values repeat themselves and the value
which occurs the maximum number of times is the modal value. The more often the modal value
appears relatively, the more variable the measure is as an average to represent data.
Example 1: Find Mode from the following data:
110, 120, 130, 120, 110, 140, 130, 120, 140, 120
Solution:
Value Tally Bars Frequency
110 || 2
120 |||| 4
130 || 2
140 || 2
Total 10

LOVELY PROFESSIONAL UNIVERSITY 61