Page 71 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 5: Application of Mean, Median and Mode

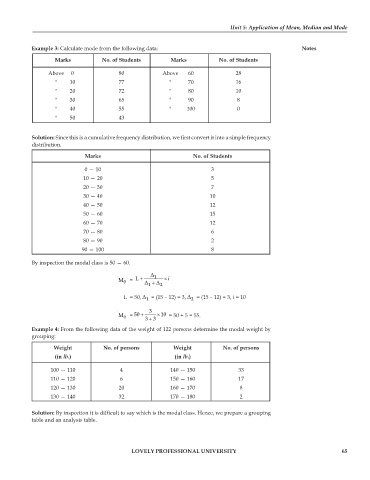
Example 3: Calculate mode from the following data: Notes

Marks No. of Students Marks No. of Students
Above 0 80 Above 60 28
" 10 77 " 70 16
" 20 72 " 80 10
" 30 65 " 90 8
" 40 55 " 100 0
" 50 43

Solution: Since this is a cumulative frequency distribution, we first convert it into a simple frequency
distribution.

Marks No. of Students
0 — 10 3
10 — 20 5
20 — 30 7
30 — 40 10
40 — 50 12
50 — 60 15
60 — 70 12
70 — 80 6
80 — 90 2
90 — 100 8

By inspection the modal class is 50 — 60.
Δ 1
M 0 = L + Δ 1 + Δ 2 × i

L = 50, Δ = (15 – 12) = 3, Δ = (15 – 12) = 3, i = 10
1
2
3
M 0 = 50 + 33 × 10 = 50 + 5 = 55.
+
Example 4: From the following data of the weight of 122 persons determine the modal weight by
grouping:
Weight No. of persons Weight No. of persons
(in lb.) (in lb.)

100 — 110 4 140 — 150 33
110 — 120 6 150 — 160 17
120 — 130 20 160 — 170 8
130 — 140 32 170 — 180 2

Solution: By inspection it is difficult to say which is the modal class. Hence, we prepare a grouping
table and an analysis table.

LOVELY PROFESSIONAL UNIVERSITY 65