Page 73 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 5: Application of Mean, Median and Mode

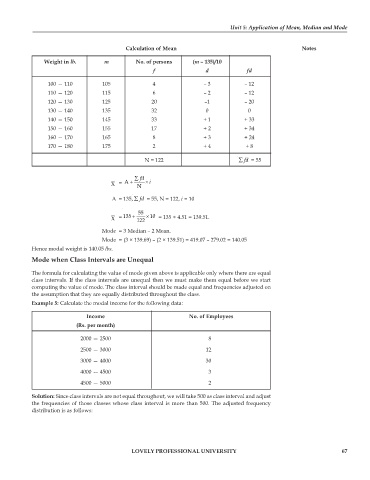
Calculation of Mean Notes

Weight in lb. m No. of persons (m – 135)/10
f d fd

100 — 110 105 4 – 3 – 12
110 — 120 115 6 – 2 – 12
120 — 130 125 20 –1 – 20
130 — 140 135 32 0 0
140 — 150 145 33 + 1 + 33
150 — 160 155 17 + 2 + 34
160 — 170 165 8 + 3 + 24
170 — 180 175 2 + 4 + 8
N = 122 ∑ fd = 55

∑ fd
X = A + N × i

A = 135, ∑ fd = 55, N = 122, i = 10

55
X = 135 + 122 × 10 = 135 + 4.51 = 139.51.

Mode = 3 Median – 2 Mean.
Mode = (3 × 139.69) – (2 × 139.51) = 419.07 – 279.02 = 140.05
Hence modal weight is 140.05 lbs.
Mode when Class Intervals are Unequal

The formula for calculating the value of mode given above is applicable only where there are equal
class intervals. If the class intervals are unequal then we must make them equal before we start
computing the value of mode. The class interval should be made equal and frequencies adjusted on
the assumption that they are equally distributed throughout the class.
Example 5: Calculate the modal income for the following data:

Income No. of Employees
(Rs. per month)

2000 — 2500 8

2500 — 3000 12
3000 — 4000 30
4000 — 4500 3
4500 — 5000 2

Solution: Since class intervals are not equal throughout, we will take 500 as class interval and adjust
the frequencies of those classes whose class interval is more than 500. The adjusted frequency
distribution is as follows:

LOVELY PROFESSIONAL UNIVERSITY 67