Page 224 - DMTH401_REAL ANALYSIS

Real Analysis

Notes 17.5 Continuous but Nowhere Differentiable Function

Theorem 7: There is a function f :  ®  which is continuous but nowhere differentiable.
Proof: The idea of a proof is to find a function with a kind of fractal behaviour. Let g(x) = |x| on
[–1, 1] extended by 2-periodicity on  and let

¥ æ 3 ö n
f(x) = å ç ÷ g (4 x )
n
è
n = 0 4 ø
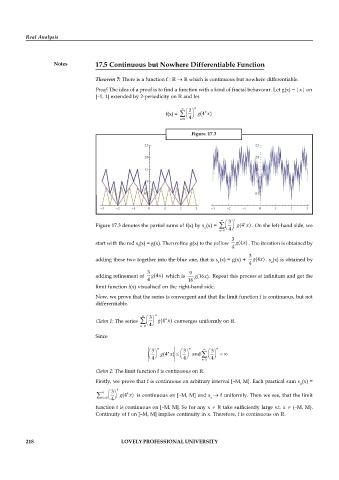
Figure 17.3

¥ 3 ö i
Figure 17.3 denotes the partial sums of f(x) by s (x) = å æ ç ÷ g (4 ) . On the left-hand side, we
i
x
è
n 0 4 ø
n =
3
x
start with the red s (x) = g(x). Then refine g(x) to the yellow g (4 ) . The iteration is obtained by
0 4
3
x
adding these two together into the blue one, that is s (x) = g(x) + g (4 ) . s (x) is obtained by
1 4 2
3 9
x
adding refinement of g (4 ) which is g (16 ). Repeat this process at infinitum and get the
x
4 16
limit function f(x) visualised on the right-hand side.
Now, we prove that the series is convergent and that the limit function f is continuous, but not
differentiable.
¥ æ 3 ö n
n
Claim 1: The series å ç ÷ g (4 x converges uniformly on .
)
è
n = 0 4 ø
Since
n n ¥ n
æ 3 ö n æ 3 ö æ 3 ö
ç ÷ g (4 x ) £ ç ÷ and å 0 4 ø < ¥
ç ÷
è
4 ø
è
è
4 ø
n
=
Claim 2: The limit function f is continuous on .
Firstly, we prove that f is continuous on arbitrary interval [–M, M]. Each practical sum s (x) =
n
k
n æ 3 ö k
)
ç ÷ g
å k 1 è ø (4 x is continuous on [–M, M] and s ® f uniformly. Then we see, that the limit
n
= 4
function f is continuous on [–M, M]. So for any x Î  take sufficiently large s.t. x Î (–M, M).
Continuity of f on [–M, M] implies continuity in x. Therefore, f is continuous on .
218 LOVELY PROFESSIONAL UNIVERSITY