Page 225 - DMTH401_REAL ANALYSIS

Unit 17: Uniform Convergence and Differentiability

Claim 3: The limit function f is not differentiable. Notes
Let x Î . Let us show that f is not differentiable at x. We will construct a sequence h , such that
m
h ® 0 and
m
x
f ( + h m )- f ( ) ® ¥ as m ® ¥
x
h m
1
1
m
Consider interval (4 x – 2 , 4 x + 2 ]. Clearly, it is a half-closed interval of length 1 and
m
therefore, can contain, only 1 integer. Define
m
m
1
ì+ 1 2 4 -m , if there is no integer in (4 x , 4 x )
+
ï
2
h = í
m 1 -m m 1 m
ï î - 2 4 , if there is no integer in (4 x , - 2 , 4 x )
We see that h ® 0 as m ® ¥. Let us define a as
m n
n n n
x
æ 3 ö g (4 ( + h )) - g (4 x )
a = ç ÷ m .
n è 4 ø h
m
Then we can rewrite the derivative as
x
f ( + h ) - f ( ) ¥
x
m a .
= å n
h
m n = 0
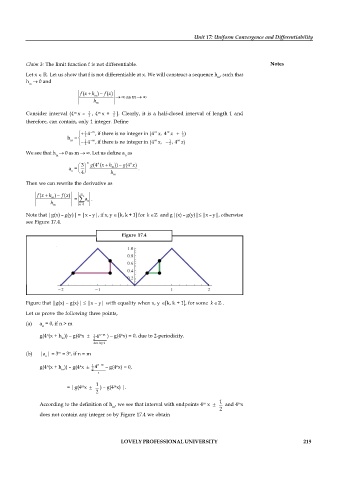
Note that |g(x) – g(y)| = |x – y|, if x, y Î [k, k + 1] for Îk  and g|(x) – g(y)|£ |x – y|, otherwise
see Figure 17.4.
Figure 17.4

Figure that |g(x) – g(x)| £ |x – y| with equality when x, y Î[k, k + 1], for some Îk  .
Let us prove the following three points,
(a) a = 0, if n > m
n
n
n
n
1
g(4 (x + h )) – g(4 x ± 4 n -m ) – g(4 x) = 0, due to 2-periodicity.
2
m 
div. by 2
m
n
(b) |a | = 3 = 3 , if n = m
n
n n 1 4 n -m n
g(4 (x + h )) – g(4 x ± 2  – g(4 x) = 0,
m
= 1
1
= |g(4 x ± ) – g(4 x) |.
m
m
2
1
m
m
According to the definition of h , we see that interval with endpoints 4 x ± and 4 x
m
2
does not contain any integer so by Figure 17.4 we obtain
LOVELY PROFESSIONAL UNIVERSITY 219