Page 226 - DMTH401_REAL ANALYSIS

Real Analysis

Notes 1 1 1
m
m
m
m
g (4 x ± )- g (4 x ) = 4 x ± - 4 x =
2 2 2
and finally
m
æ 3 ö 1 1 m n
a n = ç ÷ 2 2 1 4 m = 3 = 3
è
4 ø
n
n
(c) a n £ 3 , if < m .
1 1 1
m
n
n
n
|g(4 (x + h )) – g(4 x)| = |g(4 x ± 4 n–m ) – g(4 x)| £ |4 x ± 4 n–m – 4 x|= 4 n–m ,
n
m
m 2 2 2
and therefore
n
æ 3 ö m n 1 1 n
-
a £ ç ÷ 4 = 3
è 4 ø 2 4 m
n 1
2
Putting all things together we get
x
x
f ( + h ) - f ( ) ¥
m a = a + ...+ a +a + a + ... =
+
2
1
m
+
m
= å n 1 m 
h
m n = 0
= 0 by (a)
= ||a + a + ... +a ³ |a | – |a +... + a | ³
1 2 m m 1 m–1
by(b)
... ³|a | – |a | – |a | – ... – |a | = 3 –|a | – |a | – ... –|a | ³
m
m 1 2 m–1 1 2 m–1
by(c) 3 - 3 3
m
m
2
1
m
³ 3 – 3 – 3 – ... – 3 m–1 = 3 – = (3 m - 1 - 1) ® ¥ .

3 1 2
-
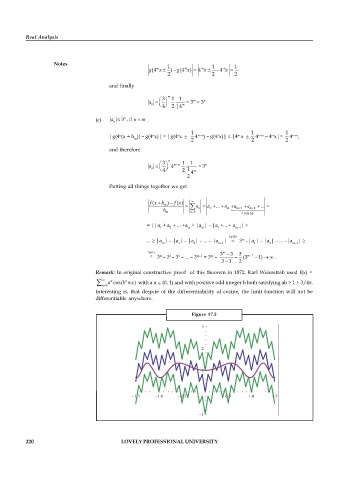
Remark: In original constructive proof of this theorem in 1872, Karl Weierstrab used f(x) =
¥ n n
a cos(b p ) x with a a Î (0, 1) and with positive odd integer b both satisfying ab > 1 + 3/4p.
å n 0
=
Interesting is, that despite of the differentiability of cosine, the limit function will not be
differentiable anywhere.
Figure 17.5

220 LOVELY PROFESSIONAL UNIVERSITY