Page 301 - DMTH401_REAL ANALYSIS

Unit 25: Mean Value Theorem

Since f is continuous in [a, b], it attains its bounds and it also attains every value between the Notes
bounds. Consequently, there is a point c Π[a, b] such that
b
Ú f(x)dx = f(c) (b a),
-
a
which, equivalently, can be written as
1 b
f(c) = Ú f(x) dx.
ba
-
a
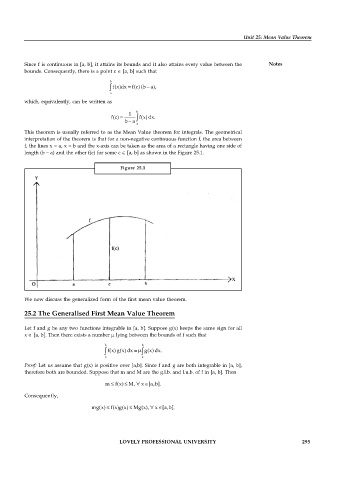
This theorem is usually referred to as the Mean Value theorem for integrals. The geometrical
interpretation of the theorem is that for a non-negative continuous function f, the area between
f, the lines x = a, x = b and the x-axis can be taken as the area of a rectangle having one side of
length (b Рa) and the other f(c) for some c Π[a, b] as shown in the Figure 25.1.

Figure 25.1

We now discuss the generalized form of the first mean value theorem.

25.2 The Generalised First Mean Value Theorem

Let f and g be any two functions integrable in [a, b]. Suppose g(x) keeps the same sign for all
x Π[a, b]. Then there exists a number m lying between the bounds of f such that
b b
Ú f(x) g(x) dx =m Ú g(x) dx.
a a
Proof: Let us assume that g(x) is positive over [a,b]. Since f and g are both integrable in [a, b],
therefore both are bounded. Suppose that m and M are the g.l.b. and l.u.b. of f in [a, b]. Then

Œ
m £ f(x) M, " x [a,b].
£
Consequently,
Œ
£
mg(x) f(x)g(x) Mg(x), " x [a,b].
£

LOVELY PROFESSIONAL UNIVERSITY 295