Page 289 - DMTH402_COMPLEX_ANALYSIS_AND_DIFFERENTIAL_GEOMETRY

Complex Analysis and Differential Geometry

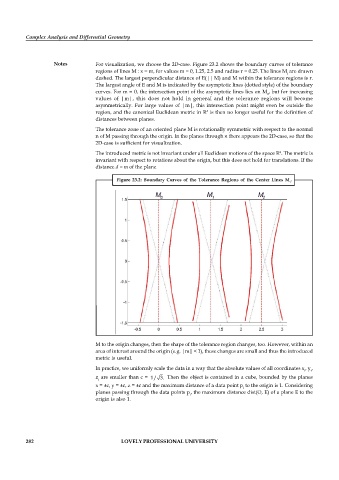
Notes For visualization, we choose the 2D-case. Figure 23.2 shows the boundary curves of tolerance
regions of lines M : x = m, for values m = 0, 1.25, 2.5 and radius r = 0.25. The lines M are drawn
i
dashed. The largest perpendicular distance of E(|| M) and M within the tolerance regions is r.
The largest angle of E and M is indicated by the asymptotic lines (dotted style) of the boundary
curves. For m = 0, the intersection point of the asymptotic lines lies on M , but for increasing
0
values of |m|, this does not hold in general and the tolerance regions will become
asymmetrically. For large values of |m|, this intersection point might even be outside the
region, and the canonical Euclidean metric in  is then no longer useful for the definition of
4
distances between planes.
The tolerance zone of an oriented plane M is rotationally symmetric with respect to the normal
n of M passing through the origin. In the planes through n there appears the 2D-case, so that the
2D-case is sufficient for visualization.

The introduced metric is not invariant under all Euclidean motions of the space  . The metric is
3
invariant with respect to rotations about the origin, but this does not hold for translations. If the
distance d = m of the plane

Figure 23.2: Boundary Curves of the Tolerance Regions of the Center Lines M .
i

M to the origin changes, then the shape of the tolerance region changes, too. However, within an
area of interest around the origin (e.g. |m| < 1), these changes are small and thus the introduced
metric is useful.
In practice, we uniformly scale the data in a way that the absolute values of all coordinates x , y , i
i
z are smaller than c = 1/ 3. Then the object is contained in a cube, bounded by the planes
i
x = ±c, y = ±c, z = ±c and the maximum distance of a data point p to the origin is 1. Considering
i
planes passing through the data points p , the maximum distance dist(O, E) of a plane E to the
i
origin is also 1.

282 LOVELY PROFESSIONAL UNIVERSITY