Page 294 - DMTH402_COMPLEX_ANALYSIS_AND_DIFFERENTIAL_GEOMETRY

Unit 23: Developable Surface Fitting to Point Clouds

We mention here that the presented curve fitting will fail in the case when inflection generators Notes
occur in the original developable shape, because inflection generators correspond to singularities
of the Blaschke image. Theoretically, we have to split the data set at an inflection generator and
run the algorithm for the parts separately and join the partial solutions. In practice, however, it
is not so easy to detect this particular situation and it is not yet implemented.

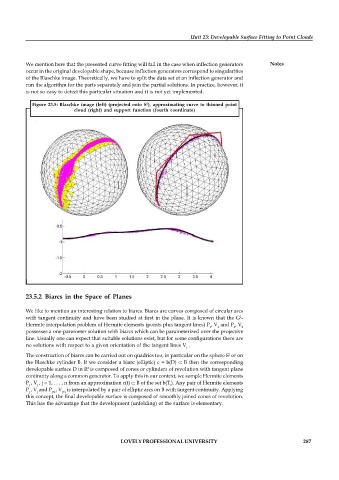
Figure 23.5: Blaschke image (left) (projected onto S ), approximating curve to thinned point
2
cloud (right) and support function (fourth coordinate)

23.5.2 Biarcs in the Space of Planes

We like to mention an interesting relation to biarcs. Biarcs are curves composed of circular arcs
with tangent continuity and have been studied at first in the plane. It is known that the G -
1
Hermite interpolation problem of Hermite elements (points plus tangent lines) P , V and P , V 2
2
1
1
possesses a one-parameter solution with biarcs which can be parameterized over the projective
line. Usually one can expect that suitable solutions exist, but for some configurations there are
no solutions with respect to a given orientation of the tangent lines V .
j
The construction of biarcs can be carried out on quadrics too, in particular on the sphere S or on
2
the Blaschke cylinder B. If we consider a biarc (elliptic) c = b(D)  B then the corresponding
developable surface D in  is composed of cones or cylinders of revolution with tangent plane
3
continuity along a common generator. To apply this in our context, we sample Hermite elements
P , V , j = 1, . . . , n from an approximation c(t)  B of the set b(T ). Any pair of Hermite elements
j
i
j
P , V and P , V is interpolated by a pair of elliptic arcs on B with tangent continuity. Applying
j
j
j+1
j+1
this concept, the final developable surface is composed of smoothly joined cones of revolution.
This has the advantage that the development (unfolding) of the surface is elementary.
LOVELY PROFESSIONAL UNIVERSITY 287