Page 39 - DMTH402_COMPLEX_ANALYSIS_AND_DIFFERENTIAL_GEOMETRY

Complex Analysis and Differential Geometry

Notes < ... < t = . Then {a = (), (t ), (t ),...,() = b} is partition of C. (Recall we assume that g’(t)  0
n
2
1
for a complex description of a curve C.) A corresponding Riemann sum looks like
n
*

S(P)   f( (t ))( (t )   (t j 1 )).

j
j

j 1

*
*
*
We have chosen the points z   (t ), where t  t  t. Next, multiply each term in the sum by
j
j–1
j
j
j
1 in disguise:
n  (t )   (t )

*

S(P)   f( (t ))( j j 1 )(t  t j 1 ).
j
j

j 1 t  t j 1
j


Hope it is now reasonably convincing that ”in the limit”, we have

 f(z)dz   f( (t)) '(t)dt.


C 
(We are, of course, assuming that the derivative ’ exists.)
Example 1: We shall find the integral of f(z) = (x + y) + i(xy) from a = 0 to b = 1 + i along
2
three different paths, or contours, as some call them.
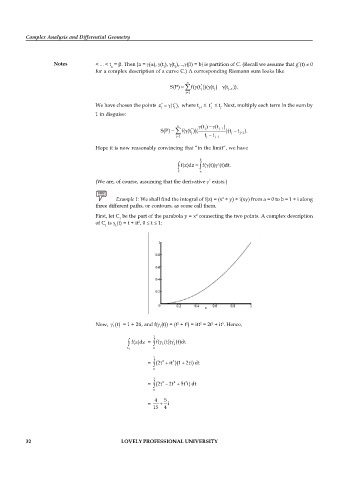
First, let C be the part of the parabola y = x connecting the two points. A complex description
2
1
of C is  (t) = t + it , 0  t  1:
2
1
1

2
3
2
2
2
Now,  ' 1 (t) = 1 + 2ti, and f( (t)) = (t + t ) = itt = 2t + it . Hence,
1
1
 f(z)dz = f( (t)) (t)dt 1  ' 1

C 1 0
1
3
2

= (2t  it )(1 2ti) dt

0
1
4
3
2

= (2t – 2t  5t i) dt
0
4 5
=  i
15 4
32 LOVELY PROFESSIONAL UNIVERSITY