Page 78 - DMTH402_COMPLEX_ANALYSIS_AND_DIFFERENTIAL_GEOMETRY

Unit 7: Transformations and Conformal Mappings

mapped on a curve with the same property in T. The correspondence between the two domains Notes
is not, however, necessarily a oneone correspondence.
For example, if we take u = x , v = y , then the domain x + y < 1 is mapped on the triangle
2
2
2
2
bounded by u = 0, v = 0, u + v = 1, but there are four points of the circle corresponding to each
point of the triangle.
7.2.1 Definition
A mapping from S to T is said to be isogonal if it has a oneone transformation which maps any
two intersecting curves of S into two curves of T which cut at the same angle. Thus, in an isogonal
mapping, only the magnitude of angle is preserved.
An isogonal transformation which also conserves the sense of rotation is called conformal
mapping. Thus, in a conformal transformation, the sense of rotation as well as the magnitude of
the angle is preserved.
The following theorem provides the necessary condition of conformity which briefly states that
if f(z) is analytic, mapping is conformal.
Theorem: Prove that at each point z of a domain D where f(z) is analytic and f(z)  0, the mapping
w = f(z) is conformal.
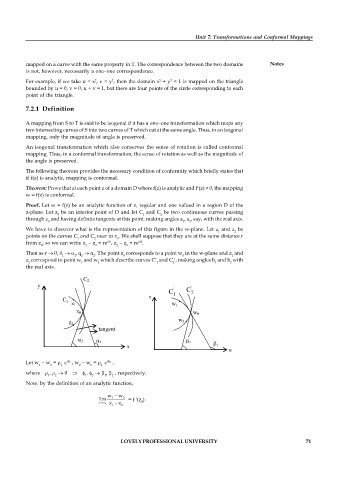
Proof. Let w = f(z) be an analytic function of z, regular and one valued in a region D of the
z-plane. Let z be an interior point of D and let C and C be two continuous curves passing
2
1
0
through z and having definite tangents at this point, making angles a , a , say, with the real axis.
1
2
0
We have to discover what is the representation of this figure in the w-plane. Let z and z be
2
1
points on the curves C and C near to z . We shall suppose that they are at the same distance r
2
1
0
from z , so we can write z  z = re , z  z = re .
i1
i2
1
0
0
0
2
Then as r  0,    , q   . The point z corresponds to a point w in the w-plane and z and
2
0
2
0
1
1
1
z correspond to point w and w which describe curves C and C , making angles b and b with
2
1
2
2
1
1
2
the real axis.
C 2
y '
'
2
C C
1
v
C 1
z 1 w 1
z 0
w 0
w 2
z 2
tangent

 2
 1  2
x  1
u
Let w  w =  e i 1 , w  w =  e i 2 ,
2
0
1
0
2
1
where  ,   0   ,    ,  , respectively.
1
2
2
1
2
1
Now, by the definition of an analytic function,
lim w  w 0 = f (z )
1
z 0 z z  z 0 0
1
LOVELY PROFESSIONAL UNIVERSITY 71