Page 267 - DMTH404_STATISTICS

Unit 18: The Weak Law

Notes
 4n 
Solution: From a deck of 4n cards, 2n cards can be chosen   in different ways. To determine
 2n 
the number of favorable draws of n red and n black cards in each half, consider the unique draw
consisting of 2n red cards and 2n black cards in each half. Among those 2n red cards, n of them

 2n   2n 
can be chosen in   different ways; similarly for each such draw there are   ways of
 n   n 
choosing n black cards. Thus the total number of favorable draws containing n red and n black


 2n  2n   4n 
cards in each half are     among a total of   draws. This gives the desired probability
 n   n   2n 
p to be
n
 2n  2n 
   4
p   n  n   (2n!) .
n 4
 4n  (4n)!(n!)
 
 2n 
For large n, using Stingling’s formula we get

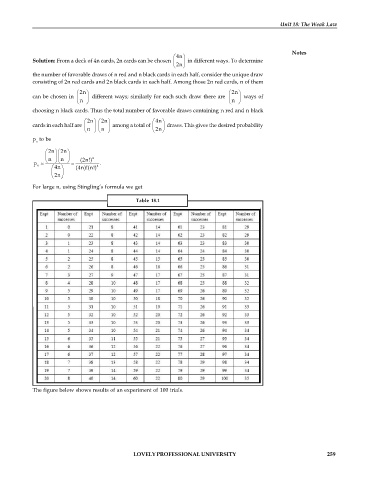
Table 18.1

The figure below shows results of an experiment of 100 trials.

LOVELY PROFESSIONAL UNIVERSITY 259