Page 432 - DMTH504_DIFFERENTIAL_AND_INTEGRAL_EQUATION

Unit 25: Volterra Equations and L Kernels and Functions
2

k Notes
x
u
y 1 ( ) f ( ) K ( , ) ( )du
f
x
x
u
0
Continuing in this manner we obtain an infinite sequence of functions
x
x
x
y
y ( ), y ( ), y ( )...... ( )...... ...(4)
x
0 1 2 n
satisfying the recurrence relations
k
u
x
u
x
x
y n ( ) f ( ) K ( , ) y n 1 ( )du , (n = 1, 2, 3....) ...(5)
0
Setting
x
x
x
y n ( ) y n 1 ( ) n n ( ) (n = 1, 2, 3....) ...(6)
and putting
(x) = f(x), we get
0
n
x
y n ( ) v 2 ( ) ...(7)
x
v 0
x
Also n ( ) K ( , ) n 1 ( )du (n= 1, 2, 3, ...)
u
x
u
x
0
t
f
x
u
u
x
Hence 1 ( ) K ( , ) ( )du
0
t u 1
)
u
x
u
f
x
and 2 ( ) K ( , u du 1 K (u 1 , ) ( )du
1
0 0
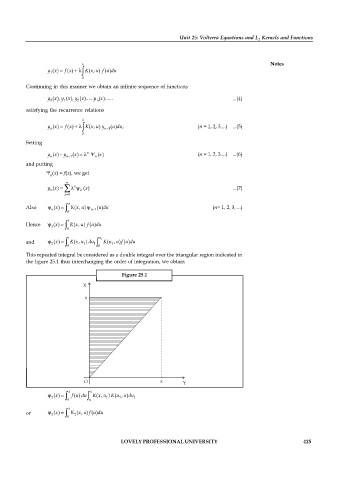
This repeated integral be considered as a double integral over the triangular region indicated in
the figure 25.1 thus interchanging the order of integration, we obtain
Figure 25.1
X
x
O x Y

x x
u
K
( ) f ( ) du K ( , u ) (u , )du
u
x
x
2 1 1 1
0 u
x
x
u
u
f
x
or 2 ( ) K 2 ( , ) ( )du
0
LOVELY PROFESSIONAL UNIVERSITY 425