Page 226 - DSOC404_METHODOLOGY_OF_SOCIAL_RESEARCH_ENGLISH

Methodology of Social Research

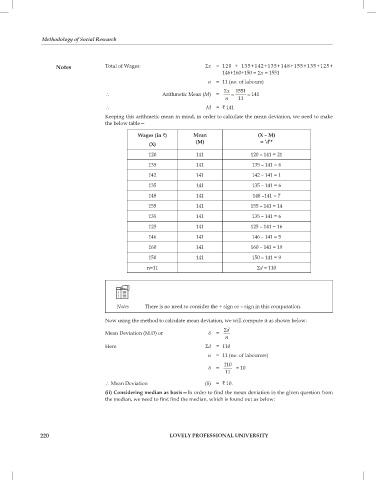
notes total of Wages: Sx = 120 + 135+142+135+148+155+135+125+
146+160+150 = Sx = 1551
n = 11 (no. of labours)
S x 1551
\ Arithmetic Mean (M) = = = 141
n 11
\ M = ` 141
Keeping this arithmetic mean in mind, in order to calculate the mean deviation, we need to make
the below table—

Wages (in `) Mean (X – M)
(x) (M) = ‘d’*

120 141 120 – 141 = 21
135 141 135 – 141 = 6
142 141 142 – 141 = 1

135 141 135 – 141 = 6
148 141 148 –141 = 7
155 141 155 – 141 = 14
135 141 135 – 141 = 6
125 141 125 – 141 = 16

146 141 146 – 141 = 5
160 141 160 – 141 = 19
150 141 150 – 141 = 9
n=11 Sd = 110

Notes there is no need to consider the + sign or – sign in this computation.

Now using the method to calculate mean deviation, we will compute it as shown below:
S d
Mean Deviation (M.D) or d =
n
Here Sd = 110
n = 11 (no. of labourers)
110
d = = 10
11
\ Mean Deviation (d) = ` 10.
(ii) considering median as basis—In order to find the mean deviation in the given question from
the median, we need to first find the median, which is found out as below:

220 loVely professional uniVersity