Page 231 - DSOC404_METHODOLOGY_OF_SOCIAL_RESEARCH_ENGLISH

Unit–28: Measures of Dispersion: Standard Deviation

(ii) considering Median as basis—in order to calculate the mean deviation using arithmetic mean, notes
we first need to compute the arithmetic mean, which is computed as shown below:

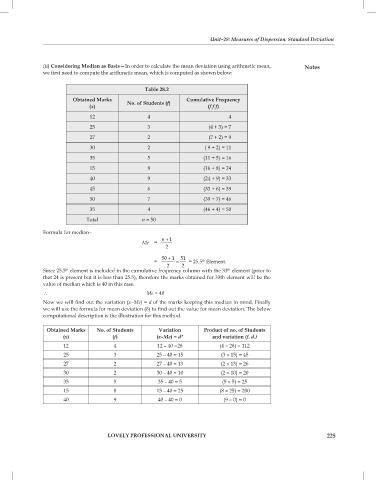
table 28.2
obtained Marks no. of students (f) cumulative frequency
(x) (f f f)
12 4 4

25 3 (4 + 3) = 7
27 2 (7 + 2) = 9
30 2 ( 9 + 2) = 11

35 5 (11 + 5) = 16
15 8 (16 + 8) = 24
40 9 (24 + 9) = 33
45 6 (33 + 6) = 39
50 7 (39 + 7) = 46

35 4 (46 + 4) = 50
total n = 50

formula for median–
n + 1
Me =
2
50 1 51
+
= = = 25.5 element.
th
2 2
since 25.5 element is included in the cumulative frequency column with the 33 element (prior to
th
th
that 24 is present but it is less than 25.5), therefore the marks obtained for 33th element will be the
value of median which is 40 in this case.
\ Me = 40
Now we will find out the variation (x–Me) = d of the marks keeping this median in mind. finally
we will use the formula for mean deviation (d) to find out the value for mean deviation. The below
computational description is the illustration for this method.

obtained Marks no. of students Variation product of no. of students
(x) (f) (x–Me) = d* and variation (f. d.)
12 4 12 – 40 =28 (4 × 28) = 112
25 3 25 – 40 = 15 (3 × 15) = 45
27 2 27 – 40 = 13 (2 × 13) = 26
30 2 30 – 40 = 10 (2 × 10) = 20
35 5 35 – 40 = 5 (5 × 5) = 25
15 8 15 – 40 = 25 (8 × 25) = 200
40 9 40 – 40 = 0 (9 × 0) = 0

loVely professional uniVersity 225