Page 230 - DSOC404_METHODOLOGY_OF_SOCIAL_RESEARCH_ENGLISH

Methodology of Social Research

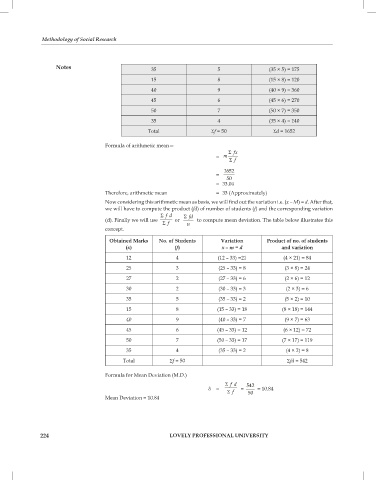
notes 35 5 (35 × 5) = 175
15 8 (15 × 8) = 120

40 9 (40 × 9) = 360
45 6 (45 × 6) = 270
50 7 (50 × 7) = 350

35 4 (35 × 4) = 140
total Sf = 50 Sd = 1652

formula of arithmetic mean—
S fx
= m
S f
1652
= 50
= 33.04
therefore, arithmetic mean = 33 (Approximately)
Now considering this arithmetic mean as basis, we will find out the variation i.e. (x – M) = d. After that,
we will have to compute the product (fd) of number of students (f) and the corresponding variation
S f d S fd
(d). finally we will use or to compute mean deviation. the table below illustrates this
S f n
concept.

obtained Marks no. of students Variation product of no. of students
(x) (f) x – m = d and variation
12 4 (12 – 33) =21 (4 × 21) = 84
25 3 (25 – 33) = 8 (3 × 8) = 24

27 2 (27 – 33) = 6 (2 × 6) = 12
30 2 (30 – 33) = 3 (2 × 3) = 6
35 5 (35 – 33) = 2 (5 × 2) = 10
15 8 (15 – 33) = 18 (8 × 18) = 144

40 9 (40 – 33) = 7 (9 × 7) = 63
45 6 (45 – 33) = 12 (6 × 12) = 72
50 7 (50 – 33) = 17 (7 × 17) = 119
35 4 (35 – 33) = 2 (4 × 2) = 8

total Sf = 50 Sfd = 542

formula for Mean Deviation (M.D.)
S f d 542
d = = = 10.84
S f 50
Mean Deviation = 10.84

224 loVely professional uniVersity