Page 164 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 8: Assignment Problem – Unbalanced

3. When an assignment problem has more than one solution, then it is Notes
(a) Multiple Optimal solution (b) The problem is unbalanced
(c) Maximization problem (d) Balanced problem

8.4 Unbalanced Assignment Problem

If the given matrix is not a square matrix, the assignment problem is called an unbalanced
problem. In such type of problems, add dummy row(s) or column(s) with the cost elements as
zero to convert the matrix as a square matrix. Then the assignment problem is solved by the
Hungarian method.

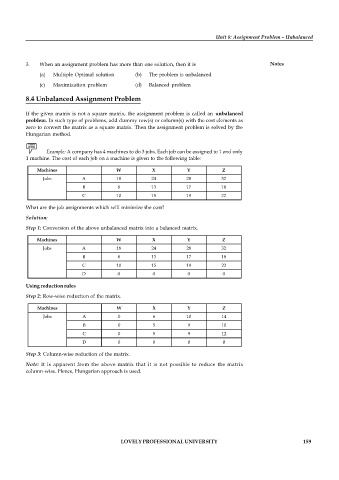
Example: A company has 4 machines to do 3 jobs. Each job can be assigned to 1 and only
1 machine. The cost of each job on a machine is given to the following table:

Machines W X Y Z
Jobs A 18 24 28 32
B 8 13 17 18
C 10 15 19 22

What are the job assignments which will minimize the cost?
Solution:

Step 1: Conversion of the above unbalanced matrix into a balanced matrix.
Machines W X Y Z
Jobs A 18 24 28 32
B 8 13 17 18
C 10 15 19 22
D 0 0 0 0

Using reduction rules
Step 2: Row-wise reduction of the matrix.

Machines W X Y Z
Jobs A 0 6 10 14
B 0 5 9 10
C 0 5 9 12
D 0 0 0 0

Step 3: Column-wise reduction of the matrix.
Note: It is apparent from the above matrix that it is not possible to reduce the matrix
column-wise. Hence, Hungarian approach is used.

LOVELY PROFESSIONAL UNIVERSITY 159