Page 188 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 9: Game Theory

Constraints are, Notes

1
1
a X + a X + ……………. + a X  1
1
11 1 21 2 m1 m
1
a X + a X + ……………. + a X  1
1
1
12 1 22 2 m2 m
.
.
. (2)
.
.
1
a X + a X + …………… + a X  1
1
1
ln 1 2n 2 mn m
1
V x  0,; i = 1 to m
i
B’s strategies can be written as,
Min. v = Expected loss
Subject to a Y + a Y + …………….. + a Y  V
11 1 12 2 ln n
a Y + a Y + …………….. + a Y  V
21 1 22 2 2n n
.
.
. (3)
.
a Y + a Y + ……………….. + a Y  V
m1 1 m2 2 mn n
If Y = V i = 1 to n,
1
i
then the constraints can be written as,

1
1
1
a Y + a Y + ……….. + a Y  1
11 1 12 2 ln n
1
a Y + a Y + ……….. + a Y  1
1
1
21 1 22 2 2n n
.
. (4)
1
a Y + a Y + ……… + a Y  1
1
1
m1 1 m2 2 mn n
V yi  0; V i = 1 to n.
The set of inequalities (2) is dual of set (4). Solving (4) by simplex method optimal solution is
obtained.
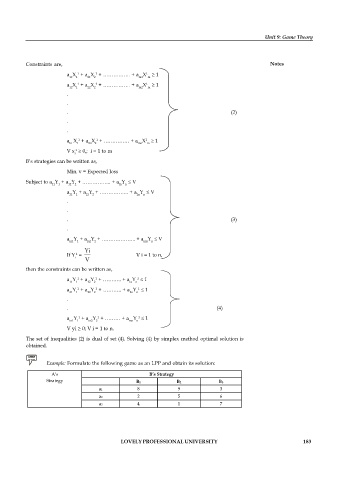
Example: Formulate the following game as an LPP and obtain its solution:
A’s B’s Strategy
Strategy B1 B2 B3

a1 8 9 3

a2 2 5 6
a3 4 1 7

LOVELY PROFESSIONAL UNIVERSITY 183