Page 61 - DCOM303_DMGT504_OPERATION_RESEARCH

Operations Research

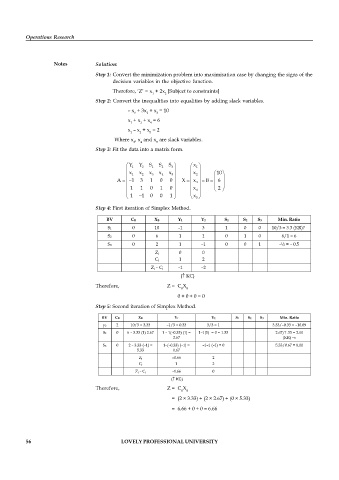
Notes Solution:
Step 1: Convert the minimization problem into maximisation case by changing the signs of the
decision variables in the objective function.

Therefore, ‘Z’ = x + 2x [Subject to constraints]
1 2
Step 2: Convert the inequalities into equalities by adding slack variables.
– x + 3x + x = 10
1 2 3
x + x + x = 6
1 2 4
x – x + x = 2
1 2 5
Where x , x and x are slack variables.
3 4 5
Step 3: Fit the data into a matrix form.

 Y 1 Y 2 S 1 S 2 S 3   x 1 
 x x x x x   x 
 1 2 3 4 5   2  10 

A   1 3 1 0 0  X   x 3   B  6 
       
 1 1 0 1 0   x 4   2 
   
 1 1 0 0 1   x 5 
Step 4: First iteration of Simplex Method.

BV CB XB Y1 Y2 S1 S2 S3 Min. Ratio
S1 0 10 –1 3 1 0 0 10/3 = 3.3 (KR)?
S2 0 6 1 1 0 1 0 6/1 = 6
S3 0 2 1 –1 0 0 1 –½ = – 0.5
Zj 0 0
Cj 1 2
Zj – Cj –1 –2
( KC)
Therefore, Z = C X
B B
0 + 0 + 0 = 0

Step 5: Second iteration of Simplex Method.
BV CB XB Y1 Y2 S1 S2 S3 Min. Ratio
y2 2 10/3 = 3.33 –1/3 = 0.33 3/3 = 1 3.33/–0.33 = –10.09
S2 0 6 – 3.33 (1) 2.67 1 – 1(–0.33) (1) = 1–1(1) = 0 = 1.33 2.67/1.33 = 2.00
2.67 (KR)
S3 0 2 – 3.33 (–1) = 1–(–0.33) (–1) = –1–1 (–1) = 0 5.33/0.67 = 8.00
5.33 0.67
Zj –0.66 2
Cj 1 2
Zj – Cj –1.66 0
( KC)
Therefore, Z = C X
B B
= (2 × 3.33) + (2 × 2.67) + (0 × 5.33)
= 6.66 + 0 + 0 = 6.66

56 LOVELY PROFESSIONAL UNIVERSITY