Page 57 - DCOM303_DMGT504_OPERATION_RESEARCH

Operations Research

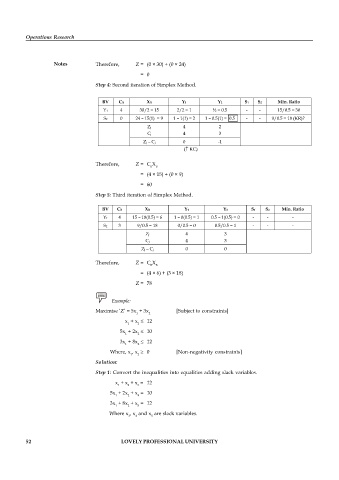
Notes Therefore, Z = (0 × 30) + (0 × 24)
= 0
Step 4: Second iteration of Simplex Method.

BV CB XB Y1 Y2 S1 S2 Min. Ratio
Y1 4 30/2 = 15 2/2 = 1 ½ = 0.5 - - 15/0.5 = 30
S2 0 24 – 15(1) = 9 1 – 1(1) = 2 1 – 0.5(1) = 0.5 - - 9/0.5 = 18 (KR)?
Zj 4 2
Cj 4 3
Zj – Cj 0 -1
( KC)

Therefore, Z = C X
B B
= (4 × 15) + (0 × 9)
= 60
Step 5: Third iteration of Simplex Method.

BV CB XB Y1 Y2 S1 S2 Min. Ratio
Y1 4 15 – 18(0.5) = 6 1 – 0(0.5) = 1 0.5 – 1(0.5) = 0 - - -
S2 3 9/0.5 = 18 0/0.5 = 0 0.5/0.5 = 1 - - -
Zj 4 3
Cj 4 3
Zj – Cj 0 0

Therefore, Z = C X
B B
= (4 × 6) + (3 × 18)

Z = 78

Example:
Maximise ‘Z’ = 5x + 3x [Subject to constraints]
1 2
x + x  12
1 2
5x + 2x  10
1 2
3x + 8x  12
1 2
Where, x , x  0 [Non-negativity constraints]
1 2
Solution:
Step 1: Convert the inequalities into equalities adding slack variables.
x + x + x = 12
1 2 3
5x + 2x + x = 10
1 2 4
3x + 8x + x = 12
1 2 5
Where x , x and x are slack variables.
3 4 5

52 LOVELY PROFESSIONAL UNIVERSITY