Page 58 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 3: Linear Programming Problem – Simplex Method

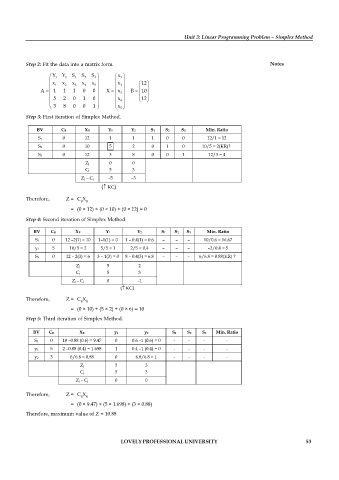
Step 2: Fit the data into a matrix form. Notes
 Y 1 Y 2 S 1 S 2 S 3   x 1 
 x x x x x   x 
 1 2 3 4 5   2  12 

A   1 1 1 0 0  X   x 3  B  10 
       
 5 2 0 1 0   x 4   12 
   
 3 8 0 0 1   x 5 
Step 3: First iteration of Simplex Method.

BV CB XB Y1 Y2 S1 S2 S3 Min. Ratio
S1 0 12 1 1 1 0 0 12/1 = 12
S2 0 10 5 2 0 1 0 10/5 = 2(KR)?
S3 0 12 3 8 0 0 1 12/3 = 4
Zj 0 0
Cj 5 3
Zj – Cj –5 –3
( KC)

Therefore, Z = C X
B B
= (0 × 12) + (0 × 10) + (0 × 12) = 0

Step 4: Second iteration of Simplex Method.
BV CB XB Y1 Y2 S1 S2 S3 Min. Ratio
S1 0 12 –2(1) = 10 1–1(1) = 0 1 – 0.4(1) = 0.6 – – – 10/0.6 = 16.67
y1 5 10/5 = 2 5/5 = 1 2/5 = 0.4 – – – –2/0.4 = 5
S3 0 12 – 2(3) = 6 3 – 1(3) = 0 8 – 0.4(3) = 6.8 – – – 6/6.8 = 0.88(KR) ?
Zj 5 2
Cj 5 3
Zj – Cj 0 –1
( KC)
Therefore, Z = C X
B B
= (0 × 10) + (5 × 2) + (0 × 6) = 10
Step 5: Third iteration of Simplex Method.

BV CB XB y1 y2 S1 S2 S3 Min. Ratio
S1 0 10 –0.88 (0.6) = 9.47 0 0.6 –1 (0.6) = 0 - - - -
y1 5 2 –0.88 (0.4) = 1.698 1 0.4 –1 (0.4) = 0 - - - -
y2 3 6/6.8 = 0.88 0 6.8/6.8 = 1 - - - -
Zj 5 3
Cj 5 3
Zj – Cj 0 0

Therefore, Z = C X
B B
= (0 × 9.47) + (5 × 1.698) + (3 × 0.88)
Therefore, maximum value of Z = 10.88

LOVELY PROFESSIONAL UNIVERSITY 53