Page 82 - DCOM303_DMGT504_OPERATION_RESEARCH
P. 82
Unit 3: Linear Programming Problem – Simplex Method
Second Iteration Notes
BV CB XB X1 X2 S1 S2 S3 Min. Ratio
x1 0 4 1 0 – – – –
S2 0 6 0 1 – – – 6/1 = 6
S3 0 18–4 (3) = 6 3–1 (3) = 0 2–0 (3) = 2 – – – 6/2 = 3 (KR)
Zj 3 0
Cj 3 2
Zj – Cj 0 –2
Third Iteration
BV CB XB X1 X2 S1 S2 S3 Min. Ratio
X1 3 4 1 0 – – – –
S2 0 6–3 (1) = 3 0 1–1 (1) = 0 – – – –
x2 2 6/2 = 3 0 2/2 = 1 – – – –
Zj 3 2
Cj 3 2
Zj – Cj 0 0
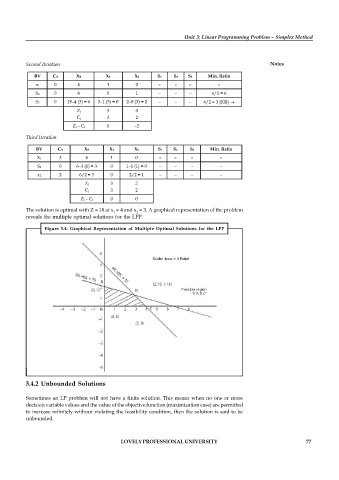
The solution is optimal with Z = 18 at x = 4 and x = 3. A graphical representation of the problem
1 2
reveals the multiple optimal solutions for the LPP.
Figure 3.4: Graphical Representation of Multiple Optimal Solutions for the LPP
3.4.2 Unbounded Solutions
Sometimes an LP problem will not have a finite solution. This means when no one or more
decision variable values and the value of the objective function (maximization case) are permitted
to increase infinitely without violating the feasibility condition, then the solution is said to be
unbounded.
LOVELY PROFESSIONAL UNIVERSITY 77