Page 84 - DCOM303_DMGT504_OPERATION_RESEARCH
P. 84
Unit 3: Linear Programming Problem – Simplex Method
Notes
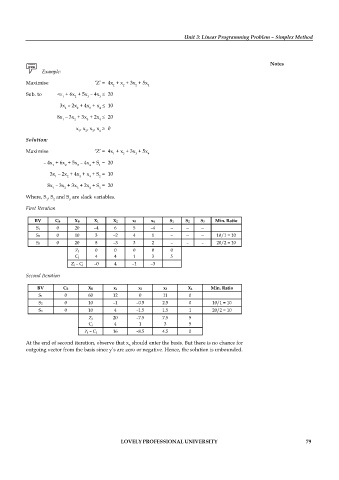
Example:
Maximise ‘Z’ = 4x + x + 3x + 5x
1 2 2 4
Sub. to – 4x + 6x + 5x – 4x 20
1 2 3 3
3x – 2x + 4x + x 10
1 2 3 4
8x – 3x + 3x + 2x 20
1 2 3 4
x , x , x , x 0
1 2 3 4
Solution:
Maximise ‘Z’ = 4x + x + 3x + 5x
1 2 3 4
– 4x + 6x + 5x – 4x + S = 20
1 2 3 4 1
3x – 2x + 4x + x + S = 10
1 2 3 4 2
8x – 3x + 3x + 2x + S = 20
1 2 3 4 3
Where, S , S and S are slack variables.
1 2 3
First Iteration
BV CB XB X1 X2 x3 x4 S1 S2 S3 Min. Ratio
S1 0 20 –4 6 5 –4 – – –
S2 0 10 3 –2 4 1 – – – 10/1 = 10
S3 0 20 8 –3 3 2 – – – 20/2 = 10
Zj 0 0 0 0 0
Cj 4 4 1 3 5
Zj – Cj –0 4 –1 –3
Second Iteration
BV CB XB x1 x2 x3 X4 Min. Ratio
S1 0 60 12 0 11 0
S2 0 10 –1 –0.5 2.5 0 10/1 = 10
S3 0 10 4 –1.5 1.5 1 20/2 = 10
Zj 20 –7.5 7.5 5
Cj 4 1 3 5
Zj – Cj 16 –8.5 4.5 0
At the end of second iteration, observe that x should enter the basis. But there is no chance for
5
outgoing vector from the basis since y’s are zero or negative. Hence, the solution is unbounded.
LOVELY PROFESSIONAL UNIVERSITY 79