Page 80 - DCOM303_DMGT504_OPERATION_RESEARCH
P. 80
Unit 3: Linear Programming Problem – Simplex Method
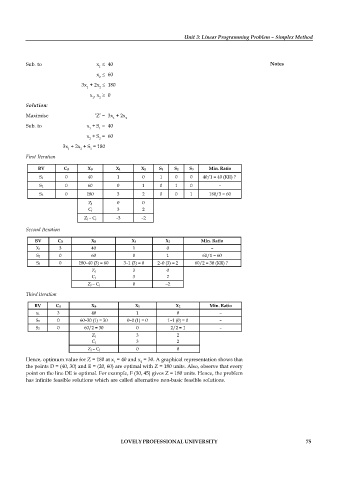
Sub. to x 40 Notes
1
x 60
2
3x + 2x 180
1 2
x , x 0
1 2
Solution:
Maximise ‘Z’ = 3x + 2x
1 2
Sub. to x + S = 40
1 1
x + S = 60
2 2
3x + 2x + S = 180
1 2 3
First Iteration
BV CB XB X1 X2 S1 S2 S3 Min. Ratio
S1 0 40 1 0 1 0 0 40/1 = 40 (KR) ?
S2 0 60 0 1 0 1 0 –
S3 0 180 3 2 0 0 1 180/3 = 60
Zj 0 0
Cj 3 2
Zj – Cj –3 –2
Second Iteration
BV CB XB X1 X2 Min. Ratio
X1 3 40 1 0 –
S2 0 60 0 1 60/1 = 60
S3 0 180–40 (3) = 60 3–1 (3) = 0 2–0 (3) = 2 60/2 = 30 (KR) ?
Zj 3 0
Cj 3 2
Zj – Cj 0 –2
Third Iteration
BV CB XB X1 X2 Min. Ratio
x1 3 40 1 0 –
S2 0 60–30 (1) = 30 0–0 (1) = 0 1–1 (0) = 0 –
S3 0 60/2 = 30 0 2/2 = 1 –
Zj 3 2
Cj 3 2
Zj – Cj 0 0
Hence, optimum value for Z = 180 at x = 40 and x = 30. A graphical representation shows that
1 2
the points D = (40, 30) and E = (20, 60) are optimal with Z = 180 units. Also, observe that every
point on the line DE is optimal. For example, F (30, 45) gives Z = 180 units. Hence, the problem
has infinite feasible solutions which are called alternative non-basic feasible solutions.
LOVELY PROFESSIONAL UNIVERSITY 75