Page 196 - DMGT405_FINANCIAL%20MANAGEMENT

Financial Management

Notes
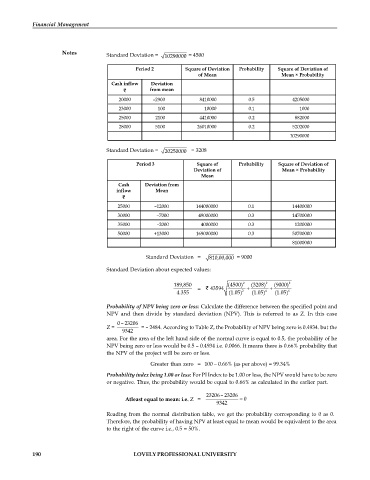
Standard Deviation = 10290000 = 4500

Period 2 Square of Deviation Probability Square of Deviation of
of Mean Mean × Probability
Cash inflow Deviation
from mean
20000 –2900 8410000 0.5 4205000
23000 100 10000 0.1 1000
25000 2100 4410000 0.2 882000
28000 5100 26010000 0.2 5202000
10290000

Standard Deviation = 20250000 = 3208

Period 3 Square of Probability Square of Deviation of
Deviation of Mean × Probability
Mean
Cash Deviation from
inflow Mean

25000 –12000 144000000 0.1 14400000
30000 –7000 49000000 0.3 14700000
35000 –2000 4000000 0.3 1200000
50000 +13000 169000000 0.3 50700000
81000000

Standard Deviation = 810,00,000 = 9000
Standard Deviation about expected values:

189,850 (4500) 2 (3208) 2 (9000) 2
= 43594  
4.355 (1.05) 2 (1.05) 4 (1.05) 6

Probability of NPV being zero or less: Calculate the difference between the specified point and
NPV and then divide by standard deviation (NPV). This is referred to as Z. In this case
0 – 23206
Z = = – 2484. According to Table Z, the Probability of NPV being zero is 0.4934. but the
9342
area. For the area of the left hand side of the normal curve is equal to 0.5, the probability of he
NPV being zero or less would be 0.5 – 0.4934 i.e. 0.0066. It means there is 0.66% probability that
the NPV of the project will be zero or less.

Greater than zero = 100 – 0.66% (as per above) = 99.34%
Probability index being 1.00 or less: For PI Index to be 1.00 or less, the NPV would have to be zero
or negative. Thus, the probability would be equal to 0.66% as calculated in the earlier part.

23206 – 23206
Atleast equal to mean: i.e. Z =  0
9342
Reading from the normal distribution table, we get the probability corresponding to 0 as 0.
Therefore, the probability of having NPV at least equal to mean would be equivalent to the area
to the right of the curve i.e., 0.5 = 50%.

190 LOVELY PROFESSIONAL UNIVERSITY