Page 152 - DMTH201_Basic Mathematics-1
P. 152
Unit 5: Equations of Straight Lines
Notes
Tasks
1. Reduce the following equations into intercept form and find their intercepts on the
axes.
(i) 3x + 2y 12 = 0, (ii) 4x 3y = 6, (iii) 3y +2 = 0.
2. Find the distance of the point ( 1, 1) from the line 12(x + 6) = 5(y 2).
Example: If the lines 2x + y 3 = 0, 5x + ky 3 = 0 and 3x y 2 = 0 are concurrent, find
the value of k.
Solution:
Three lines are said to be concurrent, if they pass through a common point, i.e., point of
intersection of any two lines lies on the third line. Here given lines are
2x + y 3 = 0 ... (1)
5x + ky 3 = 0 ... (2)
3x y 2 = 0 ... (3)
Solving (1) and (3) by cross-multiplication method, we get
x y 1
or x 1,y 1.
2 3 9 4 2 3
Therefore, the point of intersection of two lines is (1, 1). Since above three lines are concurrent,
the point (1, 1) will satisfy equation (2) so that
5.1 + k .1 – 3 = 0 or k = 2.
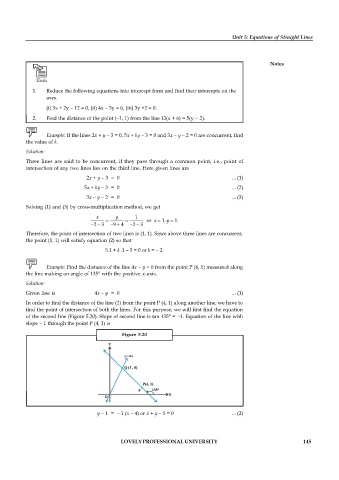
Example: Find the distance of the line 4x y = 0 from the point P (4, 1) measured along
the line making an angle of 135° with the positive x-axis.
Solution:
Given line is 4x y = 0 ... (1)
In order to find the distance of the line (1) from the point P (4, 1) along another line, we have to
find the point of intersection of both the lines. For this purpose, we will first find the equation
of the second line (Figure 5.20). Slope of second line is tan 135° = 1. Equation of the line with
slope 1 through the point P (4, 1) is
Figure 5.20
y 1 = 1 (x 4) or x + y 5 = 0 ... (2)
LOVELY PROFESSIONAL UNIVERSITY 145