Page 218 - DMTH201_Basic Mathematics-1

Unit 7: Limits

7.6.1 Limits of Important Functions Notes

(i) Prove that where n is a positive integer.

Proof: =

= n ∙ a n–1

(ii) Prove that
(a) and (b)

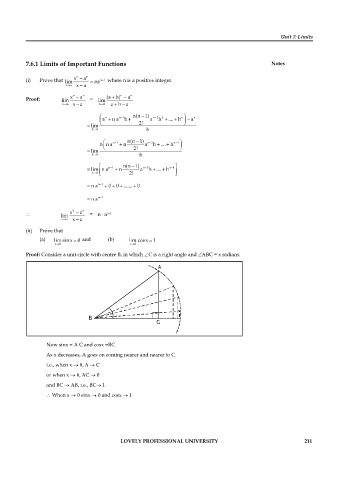
Proof: Consider a unit circle with centre B, in which C is a right angle and C = x radians.

Now sinx = A C and cosx =BC
As x decreases, A goes on coming nearer and nearer to C.

i.e., when x C
or when x C 0
and BC AB i.e., BC 1
When x 0 sinx 0 and cosx 1

LOVELY PROFESSIONAL UNIVERSITY 211