Page 213 - DMTH201_Basic Mathematics-1

Basic Mathematics – I

Notes
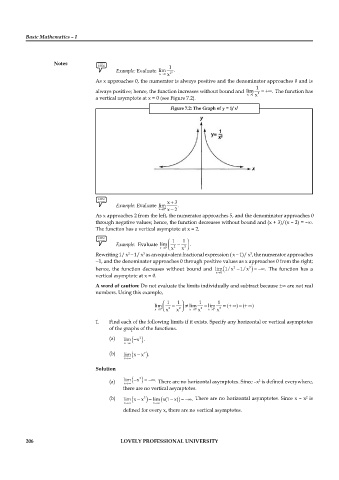
Example: Evaluate
As x approaches 0, the numerator is always positive and the denominator approaches 0 and is

always positive; hence, the function increases without bound and The function has
a vertical asymptote at x = 0 (see Figure 7.2).
Figure 7.2: The Graph of y = 1/ x 2

Example: Evaluate
As x approaches 2 from the left, the numerator approaches 5, and the denominator approaches 0
through negative values; hence, the function decreases without bound and (x + 3)/(x – 2) = – .
The function has a vertical asymptote at x = 2.

Example: Evaluate
3
2
Rewriting 1/ x 1/ x as an equivalent fractional expression ( x 1)/ x , the numerator approaches
3
−1, and the denominator approaches 0 through positive values as x approaches 0 from the right;
hence, the function decreases without bound and The function has a
vertical asymptote at x = 0.
A word of caution: Do not evaluate the limits individually and subtract because ∞ are not real
numbers. Using this example,

1. Find each of the following limits if it exists. Specify any horizontal or vertical asymptotes
of the graphs of the functions.
(a)

(b)

Solution

2

(a) There are no horizontal asymptotes. Since –x is defined everywhere,
there are no vertical asymptotes.
(b) There are no horizontal asymptotes. Since x – x is
2
defined for every x, there are no vertical asymptotes.

206 LOVELY PROFESSIONAL UNIVERSITY