Page 233 - DMTH201_Basic Mathematics-1

Basic Mathematics – I

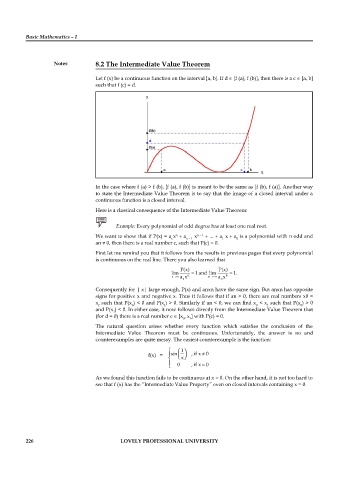
Notes 8.2 The Intermediate Value Theorem

Let f (x) be a continuous function on the interval [a, b]. If d [f (a), f (b)], then there is a c [a, b]
such that f (c) = d.

In the case where f (a) > f (b), [f (a), f (b)] is meant to be the same as [f (b), f (a)]. Another way
to state the Intermediate Value Theorem is to say that the image of a closed interval under a
continuous function is a closed interval.

Here is a classical consequence of the Intermediate Value Theorem:

Example: Every polynomial of odd degree has at least one real root.
n
We want to show that if P(x) = a x a x n – 1 ... a x a is a polynomial with n odd and
n n – 1 1 0
an 0, then there is a real number c, such that P(c) = 0.
First let me remind you that it follows from the results in previous pages that every polynomial
is continuous on the real line. There you also learned that

Consequently for | x| large enough, P(x) and anxn have the same sign. But anxn has opposite
signs for positive x and negative x. Thus it follows that if an > 0, there are real numbers x0 <

x such that P(x ) < 0 and P(x ) > 0. Similarly if an < 0, we can find x < x such that P(x ) > 0
1 0 1 0 1 0
and P(x ) < 0. In either case, it now follows directly from the Intermediate Value Theorem that
1
(for d = 0) there is a real number c [x , x ] with P(c) = 0.
0 1

The natural question arises whether every function which satisfies the conclusion of the
Intermediate Value Theorem must be continuous. Unfortunately, the answer is no and
counterexamples are quite messy. The easiest counterexample is the function:
f(x) =

As we found this function fails to be continuous at x = 0. On the other hand, it is not too hard to
see that f (x) has the “Intermediate Value Property” even on closed intervals containing x = 0.

226 LOVELY PROFESSIONAL UNIVERSITY