Page 235 - DMTH201_Basic Mathematics-1

Basic Mathematics – I

Notes This is probably the first discontinuous function you learned about. It’s called a step function,
and its domain is still the entire set of Real numbers. (The open circles mean that, for example, at
x=2, the y-value is no longer 1, but 2).

There are clearly gaps when the function jumps to each new value. You can’t run your finger
along the graph without lifting it to move to the next portion. This function is discontinuous.

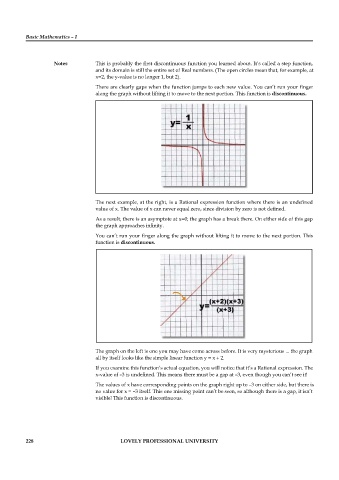
The next example, at the right, is a Rational expression function where there is an undefined

value of x. The value of x can never equal zero, since division by zero is not defined.
As a result, there is an asymptote at x=0; the graph has a break there. On either side of this gap

the graph approaches infinity.

You can’t run your finger along the graph without lifting it to move to the next portion. This
function is discontinuous.

The graph on the left is one you may have come across before. It is very mysterious ... the graph
all by itself looks like the simple linear function y = x 2.
If you examine this function’s actual equation, you will notice that it’s a Rational expression. The
x-value of –3 is undefined. This means there must be a gap at –3, even though you can’t see it!

The values of x have corresponding points on the graph right up to –3 on either side, but there is
no value for x = –3 itself. This one missing point can’t be seen, so although there is a gap, it isn’t
visible! This function is discontinuous.

228 LOVELY PROFESSIONAL UNIVERSITY