Page 236 - DMTH201_Basic Mathematics-1
P. 236
Unit 8: Continuity
Notes
There are many types of discontinuous functions, all of which exhibit one common feature ...
there is always a gap.
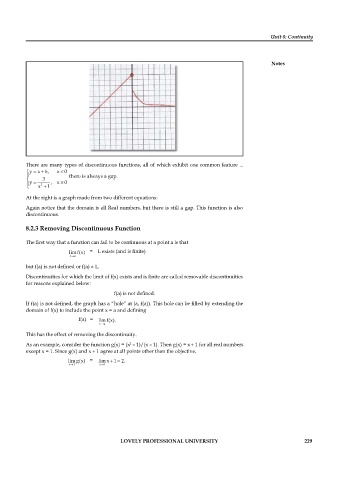
At the right is a graph made from two different equations:
Again notice that the domain is all Real numbers, but there is still a gap. This function is also
discontinuous.
8.2.3 Removing Discontinuous Function
The first way that a function can fail to be continuous at a point a is that
= L exists (and is finite)
but f(a) is not defined or f(a) L.
Discontinuities for which the limit of f(x) exists and is finite are called removable discontinuities
for reasons explained below:
f(a) is not defined.
If f(a) is not defined, the graph has a “hole” at (a, f(a)). This hole can be filled by extending the
domain of f(x) to include the point x = a and defining
f(a) =
This has the effect of removing the discontinuity.
2
As an example, consider the function g(x) = (x – 1)/(x – 1). Then g(x) = x 1 for all real numbers
except x = 1. Since g(x) and x 1 agree at all points other than the objective,
=
LOVELY PROFESSIONAL UNIVERSITY 229