Page 105 - DMTH202_BASIC_MATHEMATICS_II

Basic Mathematics-II

Notes 1  1 2  2  1 2 
Area  0    x  4 x   dx  1    1  4 x   dx

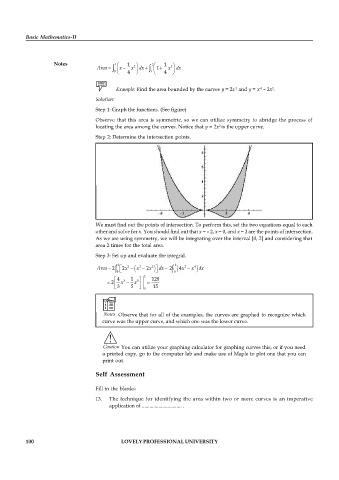
Example: Find the area bounded by the curves y = 2x and y = x – 2x .
2
2
4
Solution:
Step 1: Graph the functions. (See figure)
Observe that this area is symmetric, so we can utilize symmetry to abridge the process of
2
locating the area among the curves. Notice that y = 2x is the upper curve.
Step 2: Determine the intersection points.

We must find out the points of intersection. To perform this, set the two equations equal to each
other and solve for x. You should find out that x = – 2, x = 0, and x = 2 are the points of intersection.
As we are using symmetry, we will be integrating over the interval [0, 2] and considering that
area 2 times for the total area.

Step 3: Set up and evaluate the integral.
2 2
2
2
2
2
 dx 
Area  2 0    2x  x  2x   2 0   4x  x 4 dx
2
 4 3 1 5  128
 2 x  x 
 
 3 5  0 15
Notes Observe that for all of the examples, the curves are graphed to recognize which
curve was the upper curve, and which one was the lower curve.
!

Caution You can utilize your graphing calculator for graphing curves this, or if you need
a printed copy, go to the computer lab and make use of Maple to plot one that you can
print out.

Self Assessment

Fill in the blanks:
13. The technique for identifying the area within two or more curves is an imperative
application of ............................... .

100 LOVELY PROFESSIONAL UNIVERSITY