Page 104 - DMTH202_BASIC_MATHEMATICS_II

Unit 7: Definite Integral Applications

Step 2: Find the points of intersection. Notes
Set the two equations equal to each other.
3
2
2
2
3
y = y  y – y = 0  y (1 – y) = 0  y = 0 or y = 1
Step 3: Set up and evaluate the integral.
1 1 1 1
3
2
Area  0  y  y 3 dy  3 y  4 y 4 0
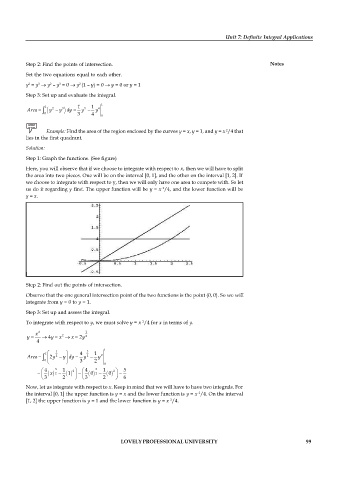
Example: Find the area of the region enclosed by the curves y = x, y = 1, and y = x /4 that
2
lies in the first quadrant.
Solution:
Step 1: Graph the functions. (See figure)
Here, you will observe that if we choose to integrate with respect to x, then we will have to split
the area into two pieces. One will be on the interval [0, 1], and the other on the interval [1, 2]. If
we choose to integrate with respect to y, then we will only have one area to compete with. So let
2
us do it regarding y first. The upper function will be y = x /4, and the lower function will be
y = x.

Step 2: Find out the points of intersection.
Observe that the one general intersection point of the two functions is the point (0, 0). So we will
integrate from y = 0 to y = 1.
Step 3: Set up and assess the integral.
2
To integrate with respect to y, we must solve y = x /4 for x in terms of y.
x 2 1
2
x
y   4y  x   2y 2
4
1
1 1  4 3 1
2
Area  0   2y   y  y 2
y dy 
2
  3 2 0
 4 3 1 2   4 3 1 2  5
0
    2    1     2    0  

x
 3 2   3 2  6
Now, let us integrate with respect to x. Keep in mind that we will have to have two integrals. For
2
the interval [0, 1] the upper function is y = x and the lower function is y = x /4. On the interval
[1, 2] the upper function is y = 1 and the lower function is y = x /4.
2
LOVELY PROFESSIONAL UNIVERSITY 99