Page 103 - DMTH202_BASIC_MATHEMATICS_II

Basic Mathematics-II

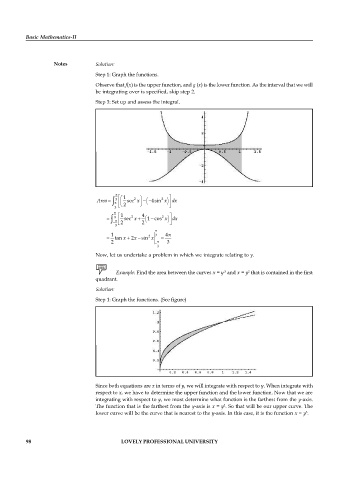
Notes Solution:
Step 1: Graph the functions.
Observe that f(x) is the upper function, and g (x) is the lower function. As the interval that we will
be integrating over is specified, skip step 2.
Step 3: Set up and assess the integral.


3  1 2  2 
Area      sec x   4sin x dx  

  2  
3
 1 4
3 
2
    sec x   1 cos x dx 2   
 
3 2 2 

1 3 4
2
 tan x  2x  sin x 
2   3
3
Now, let us undertake a problem in which we integrate relating to y.
Example: Find the area between the curves x = y and x = y that is contained in the first
3
2
quadrant.
Solution:
Step 1: Graph the functions. (See figure)

Since both equations are x in terms of y, we will integrate with respect to y. When integrate with
respect to x, we have to determine the upper function and the lower function. Now that we are
integrating with respect to y, we must determine what function is the farthest from the y-axis.
2
The function that is the farthest from the y-axis is x = y . So that will be our upper curve. The
3
lower curve will be the curve that is nearest to the y-axis. In this case, it is the function x = y .

98 LOVELY PROFESSIONAL UNIVERSITY