Page 98 - DMTH202_BASIC_MATHEMATICS_II

Unit 7: Definite Integral Applications

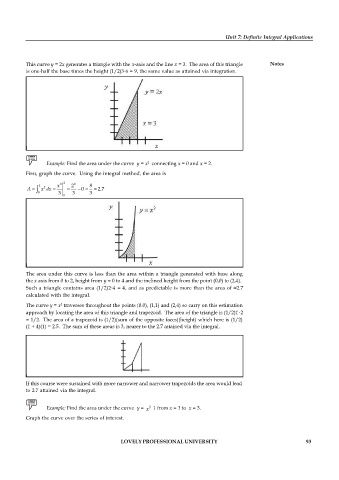
This curve y = 2x generates a triangle with the x-axis and the line x = 3. The area of this triangle Notes
is one-half the base times the height (1/2)36 = 9, the same value as attained via integration.

2
Example: Find the area under the curve y = x connecting x = 0 and x = 2.
First, graph the curve. Using the integral method, the area is
2
2 2 x 3 2 3 8
A  0  x dx    0   2.7
3
0 3 3

The area under this curve is less than the area within a triangle generated with base along
the x axis from 0 to 2, height from y = 0 to 4 and the inclined height from the point (0,0) to (2,4).
Such a triangle contains area (1/2)24 = 4, and as predictable is more than the area of 2.7
calculated with the integral.
2
The curve y = x traverses throughout the points (0.0), (1,1) and (2,4) so carry on this estimation
approach by locating the area of this triangle and trapezoid. The area of the triangle is (1/2)12
= 1/2. The area of a trapezoid is (1/2)(sum of the opposite faces)(height) which here is (1/2)
(1 + 4)(1) = 2.5. The sum of these areas is 3, nearer to the 2.7 attained via the integral.

If this course were sustained with more narrower and narrower trapezoids the area would lead
to 2.7 attained via the integral.

 3
Example: Find the area under the curve y = x 1 from x = 1 to x = 3.
Graph the curve over the series of interest.

LOVELY PROFESSIONAL UNIVERSITY 93