Page 99 - DMTH202_BASIC_MATHEMATICS_II

Basic Mathematics-II

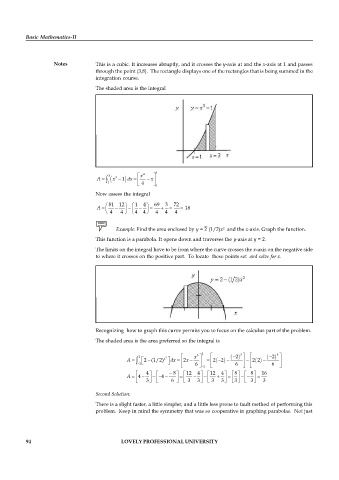
Notes This is a cubic. It increases abruptly, and it crosses the y-axis at and the x-axis at 1 and passes
through the point (3,8). The rectangle displays one of the rectangles that is being summed in the
integration course.
The shaded area is the integral

3  x 4  3
3
A  1  x   1 dx    x 
 4 1 
Now assess the integral
 81 12   1 4  69 3 72
A            18

 4 4   4 4  4 4 4
~
Example: Find the area enclosed by y = 2 (1/2)x and the x-axis. Graph the function.
2
This function is a parabola. It opens down and traverses the y-axis at y = 2.
The limits on the integral have to be from where the curve crosses the x-axis on the negative side
to where it crosses on the positive part. To locate these points set and solve for x.

Recognizing how to graph this curve permits you to focus on the calculus part of the problem.
The shaded area is the area preferred so the integral is

2 3 3
3




2 2  x    2    2 
2 (1/2) 
A      x dx   2x      2   2    2    2  

2 
 6   2   6     6  
 4    8   12 4   12 4   8   8  16
A  4    4         

  3    6     3 3   3 3      3  3
 
3 

Second Solution:
There is a slight faster, a little simpler, and a little less prone to fault method of performing this
problem. Keep in mind the symmetry that was so cooperative in graphing parabolas. Not just
94 LOVELY PROFESSIONAL UNIVERSITY