Page 96 - DMTH202_BASIC_MATHEMATICS_II
P. 96
Unit 7: Definite Integral Applications
2
The curve y = x g traverse throughout the points (0.0), (1,1) and (2,4) so persist this estimation Notes
approach by finding the area of this triangle and trapezoid grouping. The area of the triangle is
(1/2)1 × 2 = 1/2. The area of a trapezoid is (1/2)(sum of the opposite faces) (height) which for this
trapezoid is (1/2)(1 + 4)(1) = 2.5. The sum of these areas is 3.
This is an improved estimation.
!
Caution This estimation approach can be carried to superior correctness by making slighter
and slighter trapezoids.
Make the trapezoids minute enough and they get somewhat close to rectangles.
Notes Observe that this estimation strategy can be applied to any function; power,
exponential, trigonometric or any combination theorem. Therefore we have an estimation
method that can be executed out to any extent of correctness as long as we are enthusiastic
to make the comprehensive computations.
With this foreword to areas and an estimation approach to areas surrounded by functions gaze
now at what is known as the fundamental theorem of integral calculus.
2
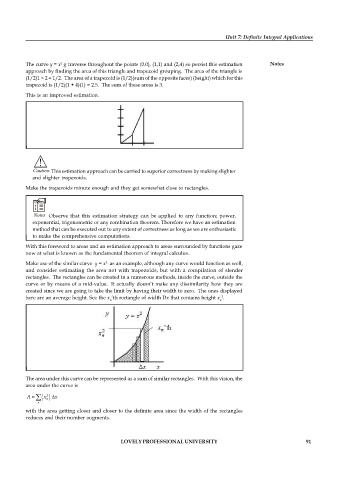
Make use of the similar curve y = x as an example, although any curve would function as well,
and consider estimating the area not with trapezoids, but with a compilation of slender
rectangles. The rectangles can be created in a numerous methods, inside the curve, outside the
curve or by means of a mid-value. It actually doesn’t make any dissimilarity how they are
created since we are going to take the limit by having their width to zero. The ones displayed
here are an average height. See the x ’th rectangle of width Dx that contains height x .
2
n n
The area under this curve can be represented as a sum of similar rectangles. With this vision, the
area under the curve is
2
x
A x
n
n
with the area getting closer and closer to the definite area since the width of the rectangles
reduces and their number augments.
LOVELY PROFESSIONAL UNIVERSITY 91