Page 211 - DCAP601_SIMULATION_AND_MODELING

Unit 12: Design and Evaluation of Simulation Experiments (II)

Notes
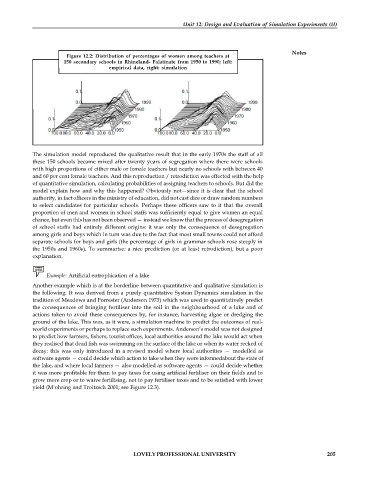
Figure 12.2: Distribution of percentages of women among teachers at
150 secondary schools in Rhineland- Palatinate from 1950 to 1990; left:
empirical data, right: simulation

The simulation model reproduced the qualitative result that in the early 1970s the staff of all
these 150 schools became mixed after twenty years of segregation where there were schools
with high proportions of either male or female teachers but nearly no schools with between 40
and 60 per cent female teachers. And this reproduction / retrodiction was effected with the help
of quantitative simulation, calculating probabilities of assigning teachers to schools. But did the
model explain how and why this happened? Obviously not—since it is clear that the school
authority, in fact officers in the ministry of education, did not cast dice or draw random numbers
to select candidates for particular schools. Perhaps these officers saw to it that the overall
proportion of men and women in school staffs was sufficiently equal to give women an equal
chance, but even this has not been observed — instead we know that the process of desegregation
of school staffs had entirely different origins: it was only the consequence of desegregation
among girls and boys which in turn was due to the fact that most small towns could not afford
separate schools for boys and girls (the percentage of girls in grammar schools rose steeply in
the 1950s and 1960s). To summarise: a nice prediction (or at least retrodiction), but a poor
explanation.

Example: Artificial eutrophication of a lake
Another example which is at the borderline between quantitative and qualitative simulation is
the following. It was derived from a purely quantitative System Dynamics simulation in the
tradition of Meadows and Forrester (Anderson 1973) which was used to quantitatively predict
the consequences of bringing fertiliser into the soil in the neighbourhood of a lake and of
actions taken to avoid these consequences by, for instance, harvesting algae or dredging the
ground of the lake. This was, as it were, a simulation machine to predict the outcomes of real-
world experiments or perhaps to replace such experiments. Anderson’s model was not designed
to predict how farmers, fishers, tourist offices, local authorities around the lake would act when
they realised that dead fish was swimming on the surface of the lake or when its water reeked of
decay: this was only introduced in a revised model where local authorities — modelled as
software agents — could decide which action to take when they were informedabout the state of
the lake, and where local farmers — also modelled as software agents — could decide whether
it was more profitable for them to pay taxes for using artificial fertiliser on their fields and to
grow more crop or to waive fertilising, not to pay fertiliser taxes and to be satisfied with lower
yield (M¨ohring and Troitzsch 2001; see Figure 12.3).

LOVELY PROFESSIONAL UNIVERSITY 205