Page 69 - DCAP603_DATAWARE_HOUSING_AND_DATAMINING
P. 69
Unit 4: Data Mining Classification
Each term in Bayes’ theorem has a conventional name: notes
1. P(A) is the prior probability or marginal probability of A. It is “prior” in the sense that it
does not take into account any information about B.
2. P(A|B) is the conditional probability of A, given B. It is also called the posterior probability
because it is derived from or depends upon the specified value of B.
3. P(B|A) is the conditional probability of B given A.
4. P(B) is the prior or marginal probability of B, and acts as a normalizing constant.
Intuitively, Bayes’ theorem in this form describes the way in which one’s beliefs about observing
‘A’ are updated by having observed ‘B’.
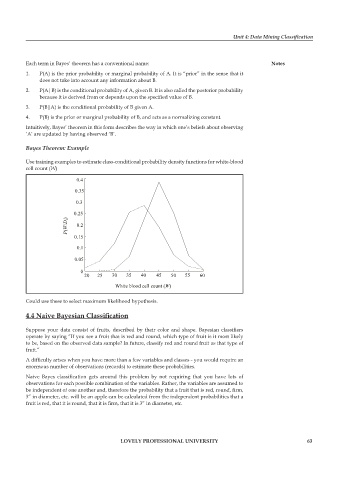
Bayes Theorem: Example
Use training examples to estimate class-conditional probability density functions for white-blood
cell count (W)
0.4
0.35
0.3
0.25
P(W/D i ) 0.2
0.15
0.1
0.05
0 20 25 30 35 40 45 50 55 60
White blood cell count (W)
Could use these to select maximum likelihood hypothesis.
4.4 Naive Bayesian Classification
Suppose your data consist of fruits, described by their color and shape. Bayesian classifiers
operate by saying “If you see a fruit that is red and round, which type of fruit is it most likely
to be, based on the observed data sample? In future, classify red and round fruit as that type of
fruit.”
A difficulty arises when you have more than a few variables and classes - you would require an
enormous number of observations (records) to estimate these probabilities.
Naive Bayes classification gets around this problem by not requiring that you have lots of
observations for each possible combination of the variables. Rather, the variables are assumed to
be independent of one another and, therefore the probability that a fruit that is red, round, firm,
3” in diameter, etc. will be an apple can be calculated from the independent probabilities that a
fruit is red, that it is round, that it is firm, that it is 3” in diameter, etc.
LoveLy professionaL university 63