Page 34 - DMGT515_PERSONAL_FINANCIAL_PLANNING

Unit 2: Time Value of Money

2.6.3 Compounded/Future Value of Series of Cash Flows [Annuity] Notes

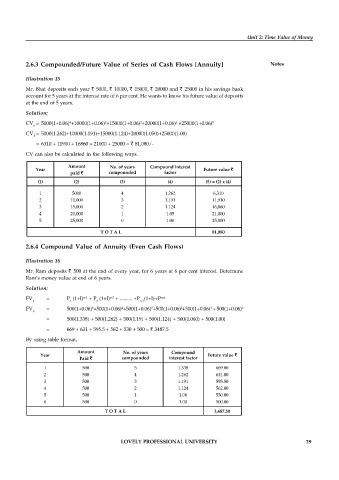
Illustration 15
Mr. Bhat deposits each year ` 5000, ` 10000, ` 15000, ` 20000 and ` 25000 in his savings bank
account for 5 years at the interest rate of 6 per cent. He wants to know his future value of deposits
at the end of 5 years.
Solution:
4
1
CV = 5000(1+0.06) +10000(1+0.06) +15000(1+0.06) +20000(1+0.06) +25000(1+0.06) 0
3
2
n
CV = 5000(1.262)+10000(1.191)+15000(1.124)+20000(1.050)+25000(1.00)
5
= 6310 + 11910 + 16860 + 21000 + 25000 = ` 81,080/-
CV can also be calculated in the following ways.
Amount No. of years Compound interest
Year Future value `
paid ` compounded factor
(1) (2) (3) (4) (5) = (2) x (4)

1 5000 4 1.262 6,310
2 10,000 3 1.191 11,910
3 15,000 2 1.124 16,860
4 20,000 1 1.05 21,000
5 25,000 0 1.00 25,000
T O T A L 81,080

2.6.4 Compound Value of Annuity (Even Cash Flows)

Illustration 16
Mr. Ram deposits ` 500 at the end of every year, for 6 years at 6 per cent interest. Determine
Ram’s money value at end of 6 years.

Solution:
FV = P (1+I) + P (1+I) + .......... +P (1+I)+P n-n
n-1
n-2
n 1 2 n-1
5
2
1
FV = 500(1+0.06) +500(1+0.06) +500(1+0.06) +500(1+0.06) +500(1+0.06) + 500(1+0.06) 0
3
4
6
= 500(1.338) + 500(1.262) + 500(1.19) + 500(1.124) + 500(1.060) + 500(1.00)
= 669 + 631 + 595.5 + 562 + 530 + 500 = ` 3487.5
By using table format,
Amount No. of years Compound
Year Future value `
Paid ` compounded interest factor
1 500 5 1.338 669.00
2 500 4 1.262 631.00
3 500 3 1.191 595.50
4 500 2 1.124 562.00
5 500 1 1.06 530.00
6 500 0 1.00 500.00
T O T A L 3,487.50

LOVELY PROFESSIONAL UNIVERSITY 29