Page 222 - DMGT524_TOTAL_QUALITY_MANAGEMENT

Unit 14: Statistical Process Control

Notes
0.1537 × 0.8463
= 0.1537 − 3
2500
= 0.1537 – 0.0242 = 0.1295.

UCL = P + 3 P (1 − P)ln = 0.1537 + 0.0242
P
= 0.1779.
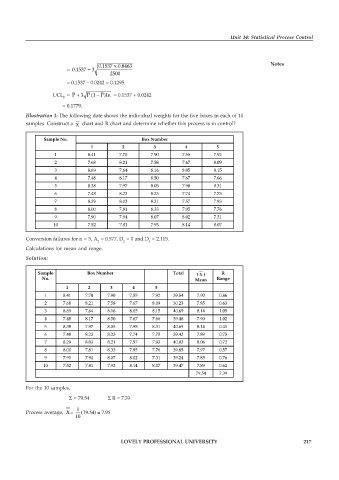
Illustration 3: The following date shows the individual weights for the five boxes in each of 10
samples. Construct a X chart and R chart and determine whether this process is in control?

Sample No. Box Number
1 2 3 4 5
1 8.41 7.70 7.90 7.55 7.92
2 7.68 8.21 7.58 7.67 8.09
3 8.69 7.64 8.16 8.05 8.15
4 7.48 8.17 8.50 7.67 7.66
5 8.38 7.97 8.05 7.98 8.31
6 7.48 8.23 8.23 7.74 7.75
7 8.29 8.03 8.21 7.57 7.93
8 8.00 7.81 8.33 7.95 7.76
9 7.90 7.94 8.07 8.02 7.31
10 7.52 7.81 7.93 8.14 8.07

Conversion failures for n = 5, A = 0.577, D = 0 and D = 2.115.
2 2 4
Calculations for mean and range.
Solution:

Sample Box Number Total ( X ) R
No. Mean Range
1 2 3 4 5
1 8.41 7.70 7.90 7.55 7.92 39.84 7.90 0.86
2 7.68 8.21 7.58 7.67 8.09 30.23 7.85 0.63
3 8.69 7.64 8.16 8.05 8.15 40.69 8.14 1.05
4 7.48 8.17 8.50 7.67 7.66 39.48 7.90 1.02
5 8.38 7.97 8.05 7.98 8.31 40.69 8.14 0.41
6 7.48 8.23 8.23 7.74 7.75 39.43 7.89 0.75
7 8.29 8.03 8.21 7.57 7.93 40.03 8.06 0.72
8 8.00 7.81 8.33 7.95 7.76 39.85 7.97 0.57
9 7.90 7.94 8.07 8.02 7.31 39.24 7.85 0.76
10 7.52 7.81 7.93 8.14 8.07 39.47 7.89 0.62
79.54 7.39

For the 10 samples,
Σ = 79.54 Σ R = 7.39
1
Process average, X= (79.54) = 7.95
10

LOVELY PROFESSIONAL UNIVERSITY 217