Page 213 - DCAP402_DCAO204_DATABASE MANAGEMENT SYSTEM_MANAGING DATABASE

Database Management Systems/Managing Database

Notes Worst case: Block transfer of STUDENT+ number of records in STUDENT * cost of searching
through index and retrieving all matching tuples for each tuple of STUDENT.
If a supporting index does not exist than it can be constructed as and when needed.

If indices are available on the join attributes of both STUDENT and MARKS, then use the relation
with fewer tuples as the outer relation.

Example: Compute the cost for STUDENT and MARKS join, with STUDENT as the outer
relation. Suppose MARKS has a primary B+-tree index on enroll no, which contains 10 entries in
each index node. Since MARKS has 10,000 tuples, the height of the tree is 4, and one more access
is needed to the actual data. The STUDENT has 2000 tuples. Thus, the cost of indexed nested loops
join as:
100 + 2000 × 5 = 10,100 disk accesses

12.4.4 Merge-join

The merge-join is applicable to equi-joins and natural joins only. It has the following process:

1. Sort both relations on their join attribute (if not already sorted).
2. Merge the sorted relations to join them. The join step is similar to the merge stage of the
sort-merge algorithm, the only difference lies in the manner in which duplicate values in
join attribute are treated, i.e., every pair with same value on join attribute must be matched.

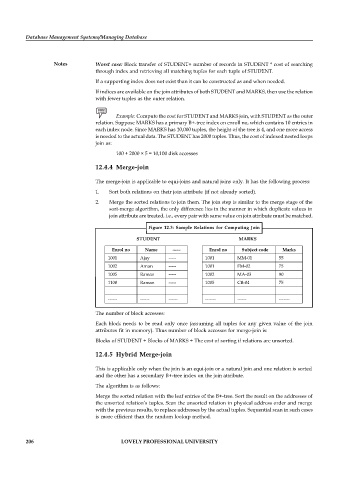
Figure 12.3: Sample Relations for Computing Join
STUDENT MARKS
Enrol no Name ----- Enrol no Subject code Marks
1001 Ajay ----- 1001 MM-01 55
1002 Aman ----- 1001 FM-02 75
1005 Raman ----- 1002 MA-03 90
1100 Raman ----- 1005 CB-04 75

------ ------ ------ ------- ------ -------

The number of block accesses:
Each block needs to be read only once (assuming all tuples for any given value of the join
attributes fit in memory). Thus number of block accesses for merge-join is:
Blocks of STUDENT + Blocks of MARKS + The cost of sorting if relations are unsorted.

12.4.5 Hybrid Merge-join

This is applicable only when the join is an equi-join or a natural join and one relation is sorted
and the other has a secondary B+-tree index on the join attribute.
The algorithm is as follows:
Merge the sorted relation with the leaf entries of the B+-tree. Sort the result on the addresses of
the unsorted relation’s tuples. Scan the unsorted relation in physical address order and merge
with the previous results, to replace addresses by the actual tuples. Sequential scan in such cases
is more efficient than the random lookup method.

206 LOVELY PROFESSIONAL UNIVERSITY